75753 IMG�81 (2)

możemy popatrzeć jak na „przeliczenie każdej niepewności o„" na „udział w a_y" wyniku pomiaru y. Oczywiście pamiętamy o założeniu, że zmienne losowe x, o odchyleniach standardowych C7_n są zmiennymi losowymi niezależnymi

Z tej samej zależności (1.20) korzystamy również, gdy wyznaczamy wypadkową niepewność typu B, w sytuacji kiedy nie ma zastosowania zależność (116) Oznacza to, że znamy odchylenia standardowe a„ wielkości r, składające się na niepewność typu B i chcemy wyznaczyć jej wypadkową wartość - 05*. Natomiast wg zależności (1 17) złożymy wypadkową wartość niepewności typu B z niepewnością typy A estymowaną przez sa.

W fizyce funkcja (1.1) jest często typu jednomianu algebraicznego, tzn. typu y— er*¹ zj’ r*’...., gdzie a, są wykładnikami. Wówczas przenoszenie błędów i przenoszenie niepewności może być rachunkiem prostszym, jeżeli działania wynikające z (1.19) i (1 20) wykonamy na wartościach względnych (wprowadziliśmy już oznaczenia składowej błędu względnego - oraz odpowiednio oznaczenia odchylenia standardowego względnego - <T* ). Wykonując odpowiednie przekształcenia (1.19) i (1.20) otrzymamy równoważne zależności (121), z których możemy korzystać, gdy wartość y była wyznaczana na podstawie jednomianu algebraicznego. Oczywiście rachunki wykonujemy na błędach względnych lub na niepewnościach względnych.

4=2 «.4

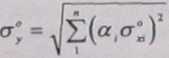
(121)

1.7. Przykłady analizy dokładności

1.7.1. Problem 1

Rezystory o wartości nominalnej /?„= 100 O wytwarzane na automacie mają rezystancję losowo zmienną, charakteryzującą się rozkładem normalnym n(/?; 100.1, 0,1). Jaki odsetek tak wytwarzanych rezystorów miałby rezystancję w granicach tolerancji ±0.1%, a jaki w granicach - ±0.2%?

Rozwiązanie Automat jest tak ustawiony, te wartość oczekiwana rezystancji ta wytwarzanych rezystorów wynosi 100.1 n, czyli nie pokrywa się z wartością nominalną. Wartość 0.1 O jest błędem ustawienia automatu. Ponadto wytwarzane rezystory charakteryzują się losowym rozrzutem wartości rezystancji, którego miara średniokwadratowa rozrzutu c% = 0.1 Cl Wyznaczenie odsetka tych rezystorów, które spełniają wymaganą tolerancję, probabilistycznie oznacza wskazanie prawdopodobieństwa P zdarzenia, że wytworzony rezystor będzie miał rezystancję z zadanego przedziału, czyli (100 tO.l) O lub (100±0.2) fl Formalnie oznacza to wyznaczenie wartości całki z funkcji gęstości rozkładu normalnego w przedziale (99.9, 100.1) lub w przedziale (99.8, 100.2), gdy wartość oczekiwana vfc“100.1fl, a odchylenie standardowe wynosi or=0,1£X Ponieważ funkcja gęstości (funkcja Gaussa) jest elementarnie niecalkowalna, więc korzystamy z kalkulatora (lub z tablic), gdzie podawane są wartości d>„ tej całki (jest to tzw funkcja Laplacc'a) dla górnej granicy całkowania, gdy dolną granicą jest zero Do korzystania z kalkulatora (lub tablic) jest konieczne jednak przejście od zmiennej losowej R do zmiennej losowej unormowanej (standaryzowanej)

Zjj=—~ ^ , bo tylko dla zmiennej w tej, uniwersalnej postaci, przygotowywane są kalkulatory (i tablice). Zgodnie z tym wykonujemy rachunki'

P = P{99.9 S RS 100.1) - d^>.(^IOOIo~*”¹] -= <M<>)-<P„(-2) - d>.(2) -0.477 =

=47.7%

P = P[99S i RS 1002} = 4^IO°y°“) -    ^ł~_[^l0°’¹j = ®.(|)-<P.(-J).034I +049* - 0*40 .

-84*/.

Odpowiedź tolerancję ±0.1% spełni około 48%, a tolerancję ±0.2% spełni 84% wytworzonych na tym automacie rezystorów.

1.7.2. Problem 2

Woltomierz o błędzie dopuszczalnym wynoszącym ±0.1% zakresu i ±0.5% wskazania sprawdzano wielokrotnie dla wskazania 2.000 V na podzakresie £4,=10 V (nominalnie). Wymienione wskazanie uzyskiwano, gdy doprowadzone do zacisków badanego woltomierza napięcie wzorcowe wynosiło kolejno U,=

2.0070, 2.0080, 2.0040, 2.0010, 2.0120, 2.0100, 2.0060 V

Dokładność wzorcowego źródła napięcia była o rząd lepsza niż badanego woltomierza.

a - Przyjmując, że stwierdzony rozrzut wyników pomiaru spowodowany jest przez zjawiska wewnętrzne badanego woltomierza wyznaczyć osobno jego składową systematyczną błędu, niepewność wyznaczenia tego błędu i jego udział w błędzie dopuszczalnym woltomierza, deklarowanym dla danego wskazania oraz osobno udział w błędzie dopuszczalnym niepewności statystycznej wskazania wyrażonej jako niepewność przedziałowa ganiczna.

b - Wyznaczyć niepewność przedziałową sprawdzanego wskazania i stosunek tej niepewności do błędu dopuszczalnego tego wskazania

c - Wyznaczyć wartości tych samych wielkości co w p. „b”, lecz przy założeniu, ze rozrzut wyników sprawdzenia powstał jako wynik zjawisk (zakłóceń) zewnętrznych w stosunku do badanego woltomierza oraz przyjąć również, że błąd dopuszczalny napięcia wzorcowego wynosił ±0.05% realizowanej wartości, a nie jak poprzednio, był pomijalny.

Rozwiązanie. Błąd dopuszczalny badanego woltomierza przedstawiono za pomocą dwu składników (bo tak przyjęło się charakteryzować dokładność cyfrowych woltomierzy)¹, które po przeliczeniu na wolty i dodaniu do siebie wyznaczają bezwzględny błąd dopuszczalny wskazania: 0.1% zakresu wynoszącego 10 V daje 0. 1-loMO-lO'² V-10 mV. a 0.5% wskazania 2.000 V daje 0.5«10'^,*2-10'¹ V-10 mV Błąd dopuszczalny badanego wskazania wynosi więc ±20 mV. Błąd dopuszczalny napięcia wzorcowego przyjmujemy równy zeru w analizie problemu a i b, ponieważ z założenia jest dziesięciokrotnie mniejszy niż błędy, które analizujemy, a więc jest nieistotny.

a - Sprawdzane wskazanie wynoszące 2.000 V uzyskiwano wielokrotnie przy napięciu o wartości różnej za każdym powtórzeniem pomiaru; średnia wartość napięcia wyniosła 2.00686 V Ocena średniokwadratowa losowego rozrzutu wartości napięcia so=0:00367 V=3.67 mV. Z obserwacji (i badali) miało wyniknąć, że ma to być rozrzut spowodowany przez zjawiska wewnętrzne badanego woltomierza, a więc taki rozrzut wynika z właściwości fizycznych lego woltomierza i jest jego charakterystyką. Równoważnie oznacza to. że przy jednym i tym samym napięciu wzorcowym utrzymywanym na zaciskach badanego woltomierza i powtarzaniu pomiaru wystąpiłby taki sam rozrzut jego wskazali.

Błąd systematyczny dla sprawdzanego wskazania wyniesie 2.000-2 00686—-Ó.00686 V“-6.86 mV, bo średnio woltomierz ten pokazuje o tyle za mało. Średniokwadratowa niepewność wyznaczenia tego błędu jest taka sama jak niepewność wyznaczenia średniego napięcia, a więc wynosi Sg =    ~ U*^{7 mV}

Ocenę przedziałową niepewności wyznaczenia błędu systematycznego określimy w sposób uproszczony

47

1

Patrz ewentualnie paragraf o niulti metrach