210(1)

Szereg może być zbieżny tylko wtedy, gdy ogólny wyraz a„ szeregu przy nieograniczonym powiększaniu się jego wskaźnika (czyli numeru porządkowego) dąży do zera, tj. gdy lim a_n = 0. Jest to warunek konieczny

n~*+ oo

zbieżności szeregu, ale nie dostateczny.

Jeśli natomiast lim a„ ^ o, to szereg jesi rozbieżny. Jest to warunek

00

dostateczny rozbieżności szeregu.

Dla szeregów o wyrazach dodatnich (a„ > 0) przy badaniu ich zbieżności stosuje się następujące warunki dostateczne (czyli kryteria) zbieżności: Kryterium całkowe Cauchy’ego. Szereg o wyrazach dodatnich malejących a„=f(n) jest zbieżny lub nie, w zależności od tego,

+ 00

czy całka niewłaściwa j f(x)dx jest zbieżna, czy też rozbieżna, gdzie

i

f( x) — malejąca funkcja ciągła¹).

Kryterium to stosuje się wtedy, kiedy istnieje taka funkcja f(x), że jej wartości dla n naturalnych pokrywają się z wyrazami badanego szeregu, czyli a_n = f(n), a która jest określona dla wszystkich x większych od pewnej dodatniej liczby a.

Kryterium d’A 1 e m b e r t a. Jeżeli lim -= g, to dla o < 1

n->+oo °ⁿ

szereg jest zbieżny, a dla q > 1 — rozbieżny. Gdy q = 1, wtedy kryterium to nie pozwala rozstrzygnąć, czy szereg jest zbieżny, czy nie.

Kryterium porównawcze. * Jeśli porównamy badany szereg o wyrazach dodatnich

0+02 + 03+ ••• +0n+ •••    (a)

z innym szeregiem o wyrazach dodatnich

^1+^2+£3+ •••    •••    (b)

którego zbieżność lub rozbieżność jest nam znana, i jeżeli poczynając od pewnego wskaźnika n:

1)    a„ < b„, to gdy szereg (b) jest zbieżny, to i szereg (a) jest zbieżny,

2)    a_n > b„, to gdy szereg (b) jest rozbieżny, to i szereg (a) jest rozbieżny. Posługując się tym kryterium badany szereg często porównuje się albo

z nieskończonym postępem geometrycznym (z szeregiem geometrycznym)

+ 00

i+s+^+gM- - = qⁿ\ q> o    (*)

n=0

■) Dolną granicą tej całki może być dowolna liczba z obszaru określoności funkcji/(a:).

zbieżny i, jak wiadomo, gdy q < 1, i rozbieżnym, gdy q ^ 1, albo też badany szereg porównuje się z rozbieżnym szeregiem harmonicznym

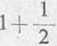
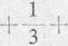
+ O0

V-¹-

n= 1

(**)

959. Sprawdzić, czy dla poniższych szeregów jest spełniony warunek konieczny zbieżności:

4- co

V;

i2m —1

y, 3«+2

2)

n=0

4-oo

V__

n= 1

--i +.L+Z+ ..

2 ¹ 5 ¹ 8 '

2/2

^{1 +} T⁺io ⁺ -

Rozwiązanie. Szukamy granicy ogólnego wyrazu szeregu dla n dążącego do plus nieskończoności. Mamy:

1) lim

n-*-+ x>

2n-\

3/I-J-2

2--

= lim--

³ + 7

2

3

2

2) lim r-r = hm-= O

«-+»«+!    ₁₄_i.

^ n-

Dla pierwszego szeregu warunek konieczny zbieżności nie jest spełniony. Szereg ten jest więc rozbieżny. Dla drugiego szeregu warunek konieczny zbieżności jest spełniony. Oznacza to, że szereg ten może być albo zbieżny, albo rozbieżny, co można ustalić dopiero w wyniku dalszego badania (patrz zadanie następne).

960. Zbadać zbieżność szeregów za pomocą kryterium całkowego:

1)

V 2 n nr+1

n — l

2)

+ 00

1

«ln’n

,.=2

-f co

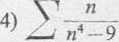
n = 3

V__L--

IŚo ł'4/J + l

3)

423