23810 str109 (5)

SU. ODWZOROWANIA KONFOREMNE 109

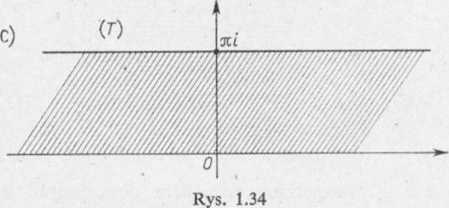
obracamy pas pionowy w płaszczyźnie (r) o kąt w kierunku trygonometrycznym. Otrzymujemy wtedy pas poziomy w płaszczyźnie (T) (rys. !.34c). Ten ostatni pasza pomocą przekształcenia

(4)    w - e¹

odwzorowujemy na górną płaszczyznę. ,

= i jest punktem wspólnym ą się przy przekształceniu (1) siebie.

i otrzymujemy ze wzoru (1) czątek współrzędnych. Przyj

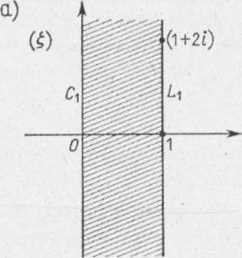
dą na prostej C₁ punkt £ = /. l oraz ( = i jest osią urojoną prostej Lj w płaszczyźnie (Q, ła do prostej C_l. Przyjmując L), otrzymujemy

powiada na prostej L_x punkt } do prostej C, (rys. 1.34a), iwuje dany obszar (zakresko-.34a). Zauważmy następnie,

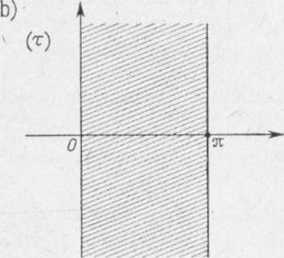
y o szerokości it (rys. 1.34 b).

,t

Składając przekształcenia (1), (2), (3) i (4), otrzymujemy funkcję, która realizuje żądane odwzorowanie. Oto ona:

* ^g * *

w = e"¹^.

Zadanie 11.13. Znaleźć funkcję homograficzną, która odwzorowuje obszar ograniczony okręgami |z-3| = 9, |z— 8| = 16 (rys. 1.35) na pierścień kołowy koncentryczny o środku w punkcie w = 0, przy czym promień okręgu zewnętrznego pierścienia winien być równy 1.

Rozwiązanie. Zauważmy przede wszystkim, że punkty tv, = 0 oraz w₂ = co są punktami symetrycznymi jednocześnie względem obu okręgów, które ograniczają pierścień kołowy, na który ma być odwzorowany nasz obszar dwuspójny. Na mocy własności symetrii w punkty = 0 oraz w₂ = co winny przejść te punkty z_L oraz z₂ płaszczyzny (z), które są symetrycznymi jednocześnie względem okręgów |z—3| = 9 oraz |z— 8| = 16. Ponieważ środki tych okręgów leżą, jak widać, na osi rzeczywistej, to punkty z, oraz z₂ powinny także leżeć na osi rzeczywistej. Wobec tego możemy przyjąć z_t = x_lt z₂ = x₂. Z jednoczesnej symetrii tych punktów względem wyżej wymienionych okręgów wynikają dwa równania

(x!-3)(x₂-3)= 81, (x₂ — 8) (x₂ — 8) = 256.

(1)