78455 str115 (5)

§11. ODWZOROWANIA KONFOREMNE 115

r₀ i 0<ę>^a_o na płaszczyźnie e w = u+iv.

waźane tutaj stacjonarne pole ami harmonicznymi. Dla zna-

-jy

r₀

:ji w(z) możemy napisać

t    'y

-arctg—. o    *

:zej z = re^i<?, to funkcje u i v

ształca prostą <p — 0 w prostą r prostą u = 0 (rys. 1.37). ly do danej zależności t(ti, o), jeratury w rozważanym pręcie

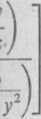
przyjmuje następującą postać:

w elektrycznym polu przepły-jbszar płaski jest ograniczony

0,

D,

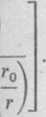
Punkty znajdujące się na luku okręgu K₃ mają potencjał V_o>0, natomiast punkty

leżące na okręgu K₃ mają potencjał równy zero. Punkty metalowej folii leżące na lukach

kół i K₂ są izolowane elektrycznie od zewnętrznej części rozważanego obszaru płaskiego.

Rozwiązać podane zagadnienie wiedząc, że funkcja

, .    . z—l

w (z) = u + w =-

z—2

przekształca rozważany obszar w kwadrat.

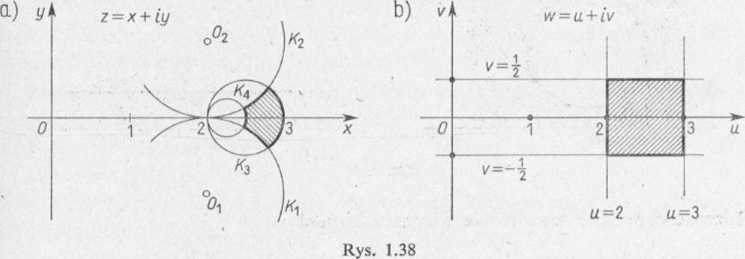
Rozwiązanie. Na wstępie zauważmy, że funkcja iv(z) przekształca okrąg K_x w prostą v = i, okrąg K₂ w prostą v = — i, okrąg K₃ w prostą u = 3 oraz okrąg K_A w prostą u = 2, co widać po rozdzieleniu funkcji w(z) na jej części rzeczywistą u i urojoną v (rys. 1.38b). Mamy bowiem z = x + iy, zatem

w (z) = u + iv

x²+y²-3x+2    . y

x² + y²—4x+4 x² + y²—4x+4‘

Potencjał ip(u, v) pola przepływowego w kwadracie 2<u<3, —$<v<% odwzorowanego przez funkcję w(z) na szukane pole spełnia następujące warunki brzegowe:

(p (3, o) = V₀,    ę(2,v) = O

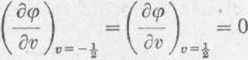
zatem (p(u,v) jest funkcją następującej postaci:

dla

dla

2<u<3,

(p{u,v)= V₀(u-2).

Jeżeli do powyższej zależności na miejsce zmiennej u podstawimy część rzeczywistą u(x, y) danej funkcji w (z), to otrzymamy funkcję <p (x, j) określającą rozkład potencjału w rozważanym płacie folii metalowej. Jest to następująca funkcja:

,    ,    „(x² + y²-3x + 2

która po prostym przekształceniu przyjmuje postać

/ x    x²+y²-5x + 6

<p{x,y) = - V₀ -₂ -

x +y — 4x+4