42869 str097 (5)

§11. ODWZOROWANIA KONFOREMNE 97

(5)

ornej pólpłaszczyźnie. Reasu-dowoiną liczbę rzeczywistą, związaniem naszego zadania

imograficzne odwzorowujące

rechodziła w prostą; równo-zero. Wobec tego przekształ-

Uwzględniając równości (3) i (4) we wzorze (2), mamy

a z—ot.

w ----.

c z+a

Aby wyznaczyć współczynnik a/c, zauważmy, że punktowi z = 0, leżącemu na osi urojonej Rez = 0, musi odpowiadać punkt okręgu |vv| = 1. Analogicznie, jak w zadaniu 11.1, wykazujemy, że

gdzie <p — dowolna liczba rzeczywista.

Podstawiając równość (6) do wzoru (5), mamy

(7)

w = e

lq>

z—a z+a'

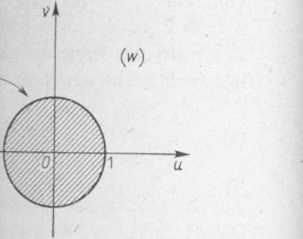
Dla z = a mamy w = 0, więc punkt a musi leżeć w prawej pólpłaszczyźnie. Reasumując, możemy powiedzieć, że wzór (7), gdzie ę — dowolna liczba rzeczywista, aa — dowolna liczba zespolona, dla której Rea>0, jest rozwiązaniem naszego zadania (rys. 1.23)

niosku, że punkty = — bla mej. Jeżeli więc

Zadanie 11.3. Znaleźć najogólniejsze odwzorowanie homograłiczne koła |z| na koło |w|<R₂*

Rozwiązanie. Szukana funkcja ma postać

(1)

az+b cz + d'

Widać od razu, że musi być a ^ 0, bo w przeciwnym razie punkt zewnętrzny z — oo przeszedłby w punkt wewnętrzny w = 0. Jednocześnie stwierdzamy, że musi być d £ 0,

7 — Wybrane dziaty matematyki...