str105 (5)

§11. ODWZOROWANIA KONFOREMNE 105

aniu (1) przechodzi w punkt rzędne tego punktu są jedna-ień r (rys. 1.26b). Ponieważ vaniem zwrotu, to aby otrzy-|t dokoła początku układu płaszczyźnie (z) po łuku y od ys. 1.26a) po prawej stronie.

Oznaczając przez z_x oraz z₂ punkty przecięcia się okręgów (1) wyliczamy

(2)

1 .V3

zx =—

Zauważmy dalej, że funkcja homograficzna

(3)

/₃

odwzorowuje punkt z₂ = £ + / — ^w punkt £ = oo, a punkt z₂ = \—i—— w punkt £ = 0.

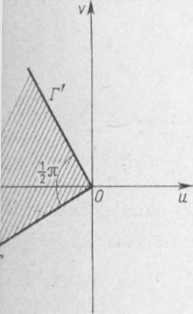
Wobec tego obszar zakreskowany (rys. 1.27) przechodzi przy odwzorowaniu (3) w kąt z wierzchołkiem w punkcie £ = 0. Wielkość tego kąta wynosi •§Jt, odczytujemy to z rysunku 1.27. Aby wyjaśnić jak położony jest ten kąt w płaszczyźnie (£), postępujemy analogicznie jak w zadaniu 11.9. W tym celu zauważamy, w co przechodzi punkt z = 1, leżący na łuk« /, ? Przyjmując we wzorze (3) z = 1, otrzymujemy

(4)

1 + i V 3 (l + '\/3)² 1 —iV3~ 4

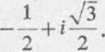
conforemnie obszar, będący 1 i promieniu 1 (rys. 1.27),

w zadaniu, są następujące:

Ze wzoru (4) wynika, że łuk /, płaszczyzny (z) przechodzi przy odwzorowaniu (3) w pół prostą L, płaszczyzny (£) wychodzącą z początku układu i przechodzącą przez punkt

/3

£ = -ł+'-y (rys. 1.28).

Zauważmy teraz, że poruszając się po łuku /, od punktu z₂ do punktu z, mamy obszar zakreskowany (rys. 1.27) po lewej ręce. Punktowi z₂ odpowiada w płaszczyźnie (£) punkt £ = 0. W konsekwencji, aby otrzymać półprostą L₂, będącą obrazem łuku /₂ przy odwzorowaniu (3), należy półprostą L_t obrócić o kąt fit w kierunku przeciwnym do ruchu wskazówek zegara (rys. 1.28), bo odwzorowanie (3) jako konforemne zachowuje kąty co do wielkości i zwrotu. Zauważmy dalej, że przekształcenie

(5)    T = £e“5ⁿ‘

odwzorowuje kąt zakreskowany w płaszczyźnie (£) na kąt zakreskowany w płaszczyźnie (T) (rys. 1.29). Widzimy, że przy przekształceniu (5) ramię L, przeszło w półprostą, która pokryła się z dodatnim kierunkiem osi rzeczywistej w płaszczyźnie (T). Aby kąt zakreskowany w płaszczynie (7) (rys. 1.29) odwzorować na górną półpłaszczyznę, wystarczy wziąć którąkolwiek gałąź przekształcenia

(5')    w = T2,

bo kąt $jt odwzorowuje się przy przekształceniu (5') w kąt

ł«‘ł = n-