58633 str099 (5)

I SU. ODWZOROWANIA KONFOREMNE    99

>y w punkt zewnętrzny w — co. iv postaci

idają w płaszczyźnie (w) w myśl r = 0 i w₂ — oo są syme-b/a oraz z₂ = ~dlc muszą być

skąd

(9)

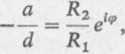
gdzie (p jest dowolną liczbą rzeczywistą.

Podstawiając równość (9) do wzoru (5), otrzymujemy po przekształceniach

(10)

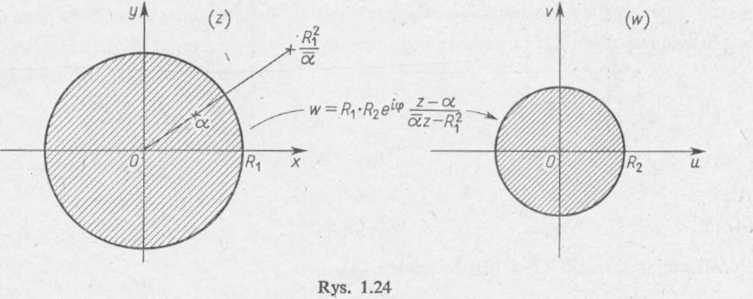
w = R_lR₂eⁱ‘^l>

z —a az—Ri'

Zauważmy na koniec, że punkt z = a musi leżeć wewnątrz koła |z| <    , bo odpowiada

jący mu punkt w = 0 leży wewnątrz koła \w\<R₂.

x

-1

ly fakt, że punktowi z =

R₂. Wobec tego ze wzoru (5)

Reasumując stwierdzamy, że wzór (10), gdzie ę oznacza dowolną liczbę rzeczywistą, a — dowolną liczbą zespoloną, dla której |a[jest rozwiązaniem naszego zadania (rys. 1.24). W szczególności funkcja

(U)

z—a. OLZ— 1*

gdzie (p jest dowolną liczbą rzeczywistą, |a| < 1, odwzorowuje koło jednostkowe |z|<l w koło jednostkowe | w\ < 1 w ten sposób, że dowolny punkt a koła \z\ < 1 przechodzi w środek koła |w|<l.

Zadanie 11.4. Znaleźć funkcję, która trójkąt prostokątny i równoramienny ABC o wierzchołkach z, = (3 + 2i), z₂ = (7+2i), Z3 = (5+4/) odwzorowuje w trójkąt prostokątny i równoramienny OB_lC_l o wierzchołkach w₁ — 0, w₂ = —2/, vv₃ = (1—i) w ten sposób, że wierzchołki z_k przechodzą odpowiednio w wierzchołki w* (k — 1,2,3), (rys. 1.25).

Rozwiązanie. Z tego, że dany trójkąt prostokątny i równoramienny ABC ma przejść w trójkąt prostokątny i równoramienny OB_lC₁ wynika, że szukana funkcja ma postać

(1)    w = az+b.

Z warunków zadania wynika kolejno

(2)    Arga = ~in,

7*