24880 zerowy2007

AGH - WYDZIAŁ IMiR ROK IE i F EGZAMIN Z MATEMATYKI TERMIN O KRAKÓW 26. 01. 2007

lim/(^JC) = ^co

l.a) Podaj definicję i ilustrację geometryczną niewłaściwej granicy lewostronnej

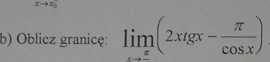
2

2.    a) Podaj definicję pochodnej funkcji y = f(x) w punkcie x₀. Oblicz z definicji

pochodną funkcji y = sinx w punkcie x = 0 .

b) Oblicz pochodną funkcji: y = (i’g2x)°®ź + arccos Vl - 3x .

3.    a) Podaj i udowodnij twierdzenie Rolle’a.

Czy teza tego twierdzenia ma zastosowanie do funkcji y = 1 i pf? w przedziale    ?

Uzasadnij odpowiedź.

b) Znajdź asymptoty funkcji : y = x Inljg + -ii

| .a) Co to znaczy, że wykres funkcji y i f(x) jest wypukły a) ku górze

b) ku dołowi?

Jak badamy wypukłość funkcji? Zacytuj odpowiednie twierdzenie, b) Wyznacz przedziały wypukłości i punkty przegięcia funkcji: y = x⁴ (l 2 ln x i 7).

w (jc\cłx

5. a) Opisz całkowanie funkcji niewymiernych typu: |    'A— , gdzie łP„(x)jest

^J Vax² +bx + c

wielomianem stopnia n - metodą czynników nieoznaczonych.

xdx

-Jlx-\0-x²

b) Oblicz całkę:    f

ć.a) Podaj I główne twierdzenie rachunku całkowego. Jaki związek ma teza tego twierdzenia z pojęciem całki nieoznaczonej? b) Przy użyciu rachunku całkowego oblicz objętość stożka obrotowego o wysokości h i promieniu podstawy r. ( RYSUNEK 1).

7.a) Co to znaczy, że punkt x = b jest punktem osobliwym funkcji y =f(x) ?

b

Podaj definicję całki niewłaściwej J f(x)dx gdy punkt x i b jest punktem osobliwym

funkcji y = /(x).

x² +1

b) Oblicz pole obszaru zawartego między wykresem funkcji y = ^ar? — i osią Ox.

dla x > 0 .