28967 P1020152

Henryk Jusfcka

Henryk Jusfcka

1	skokowe:
	H(s) = ka	h{tj — k a-S(t)		(109)
7‘ •.	1 i n i o wo-czaso we:
	G* II ??• *■» | <>	v(/j = k b-l(t)		(110)
a)		b)
h(0 ‘		w'	i
		k' b
.	1 oo	t		t ->-
		——*->• ■"^1
Rys. 29. Charakterystyki		czasowe elementu	różniczkującego	idealnego:

a) skokowa; b) liniowo-czasowa

Element różniczkujący z inercją

Rzeczywisty element różniczkujący jest układem złożonym z szeregowo połączonych elementów: inercyjnego i różniczkującego idealnego. Przykładem takiego elementu może być każde ciało poruszające się w cieczy np.: statek, tłok itp. Jeżeli za wielkość wejściową przyjmiemy pozycję tego ciała, a za wielkość wyjściową siłę oporu z jaką ciecz działa na ciało, gdy chcemy zmienić jego położenie.

Charakterystyka czasowa przedstawiona została na rys. 30. Ma on duże znaczenie praktyczne, gdyż każdy fizycznie realizowalny element różniczkujący posiada pewną inercję. Transmitancja takiego elementu przedstawia się następująco:

(111)

G(s) -

sk

1 + sT

Natomiast jego charakterystyki czasowe p_rzy wymuszeniu:

-    skokowym:

^H(I)=irir    vo-Ł*.,•*.«,)    (u

—    liniowo-czasowym:

V(#)-

kb

s(i + sT)

^v(t) = k b-a-e ' ) !(/)

(II

■)    b)

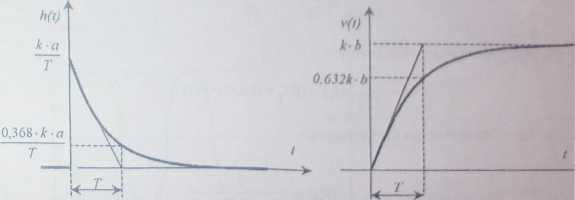
Rys. 30. Charakterystyki czasowe członu różniczkującego rzeczywistej a) skokowa; b) liniowo-czasowa

Elementem różniczkującym rzeczywistym jest czwómik z rys. 31.

C

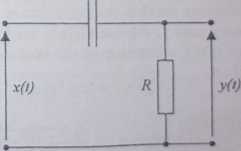
Rys. 31. Czwórnik RC różniczkujący rzeczywisty