2(17)

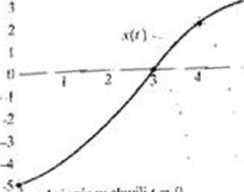
v położenie w- chwili / -» fł

a)

w sposób bardziej abstrakcyjny. Tej zależności nie można zobaczyć wprost, j'* zawiera ona więcej informacji mz sam widok poruszającego się borsuka. Możni się / niej dowiedzieć, jak szybko porusza się borsuk.

To. jak szybko porusza się czystka, możemy wyrazić w różny sposób Jedną z możliwości jest podanie średniej prędkości r„. która opisujemy stosunkiem /1%| przemieszczenia cząsiki A.v w pewnym przedziale cz.tsu Ar. do wielkości lego przedziału czasu:

A.«    xi - x_t

(2.2)

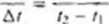
u

Zapis ten oznacza, ze cząstka jest w położeniu ,V| w chwili /_r. u potem w położeniu \t w chw ili r». Typowym przykładem jednostki e_M jest metr na sekundę (m/s) W zadaniach spotkasz. tez inne jednostki, lec? zawsze będ.| mieć one jHKiać

■*" “j"!    ¹    2~ '^,,nl ilorazu jednostki długości i jednostki czasu.    i

;    .1 / |s| Na wykresie x jako funkcji t wartość t';_r jest równa nachyleniu (współ- j

hj    czynnikowi kierunkowemu) prostej, łączącej dwa punkty na krzywej .v(0: punkt j

Rys. 2.3. a> Wykics vl/> dla p»«rus/;iją. ce*o się borsuka. In Ruch iHwsuka. ku*r> ilustruje ten wykres IW «w*-j » zaznaczono chwile, w kiórych WmmA osiąga odpowicilnie wątłości potużenu i

od|xnv lądujący wartościom i /* oraz punkt odjK>wind;ijący wartościom .Vj i ż|.

Podobnie jak przemieszczenie. ma zarówno wartość bezwzględną, jak i kierunek (jest u* niwnież wielkość wekicuowa). Wartość bezwzględna prędkości średniej jcsl równa wartości bezwzględnej nachylenia prostej Jeśli i**, a więc i nachylenie są dodatnie, to linia na wykresie wznosi się wraz ze wzrostem /,

a jeśli »<t i nachylenie są ujemne. u> linia na wykresie opada wraz ze wzrostem t ¹ Prędkość średnia tv, ma zawsze taki sam znak. jak przemieszczenie A.v. gdy/ A; wv w/oiz.e «2.2J jest zawsze dodatnie.

N'a rysunku 2.4 pokazano sposób wyznaczenia i\, dla borsuka z rysunku 2.3. I

4

i/.. «- nuchytcnic tej prostej

2

Av

3?

w przedziale czasu od / - I s do / = 4 s. Wykreślamy prostą, łączącą punkt ! na krzywej, odpowiadający początkowi tępo przedziału : punkt odpowiadający i końcow i przedziału. Następnie wyznaczamy nachylenie prostej A.v/A/ lak więc prędkość średma w zadanym przedziale czasu wynosi:

i—:t—«'i»i

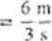
N'a pytanie, jak szybko |*>iusznłu się cząstka. możemy też odpowiedzieć w inny sposób. dzieląc przez czas nie przemieszczenie czystki Av. lecz. całkowita drogę

-4

(na juzy kład w metrach), przebytą w tym czasie przez cząstkę, niezależnie od kierunku, izn |xxlając wielkość:

Ai »2nt-(-lm) <6m

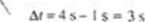
całkowita droga

Rys. 2.4 Wyzu.ic/anir średniej prędkości w przedziale czasu cxl r = I s do f = *1 x. jako nachylenia prostej, łączącej punkty na krzywej *(i). odpowiadające tym chwilom

(2.3)

Wielkość ta rur uwzględnia kierunku ruchu (mając w istocie znaczenie średniej wartości bezwzględnej prędkości), zatem me ma znaku. Czasem jest ona równa

wartości bezwzględnej i\,. ale — jak (Kłkażcmy w przykładzie 2.1 — może się od niej bardzo różnić, gdy ciało porusza się dwa razy po lej samej drodze Wielkość tę nazywamy czasem prędkością „podróżną".

16    2. Ruch prostoliniowy

Aa,

'' ~ r„, ~ (70 km/h)

m 0.12 h.

Wobec tego^-Ar = Ar,

f;

(odiwwicdż

SPRAWDZIAN 2: Załóżmy. *e p.

luku powróciłeś do punktu aj i pręrlkuści nosiła śierlnia pnędkuśc całej podróży?

2 .3 Pr

0.4

czucsl h]

0.6

Przykład 2.1

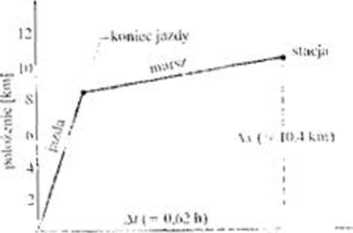
JtChałci Mar.t furgonetką pi> pioslcj drodze. z prędkością 70 knVh R> przebyciu ilmji 8.4 km skotk/yla ci su; benzyna i samochód śę utrzymał. Musiałeś wiyc im. pics/o - km <to iwiMi/s/cj stacji tMflynnuej. co zajęło ci .V) minut.

*)l!e wynosiło twoje całkowite przcmics/c/cmc od początku po

dróiy Ai stacji benzynowej?

KJZWlĄZANię

Załóżmy illa wygody, że poruszałeś sic ^vv dodatnim kierunku osi a. od położenia jtiK/.iikowcgo i, -O do pulo/cnia »• Twoje położone Wmmo to «■;    S.4 km + 2 km lt» I km O—*

Twx>jc pr/emu szczenię wzdłuż osi v jest równe ló/mcy położenia końcowego i poc/tukowcgo /. lównunia (2 1' «Hr/\ mnjem\

A.v = \>    ,i| s= 141.4 kin t) — 10.4 km lodpowicd/i

Tak wi_vv twoje całkowite przemieszczenie było równe 10.4 km w dodatnim kierunku osi i

b) Dc czasu Nr upłynęło od poc/atku p.Hltóży.do chwili przybycia u Kacie łvii/\nnvą?

fcOZWIĄlANIE

Znamy juz t/.is inurs/o A/_m. nVw-ny (1.5 li. ale nic znamy czasu jazdy vaniivluik.ni Ar, Wiemy jednak. zc w czasie ja/dv przemieściłeś sic <■ Ai,. wynoszące 8.4 km. waz że średnia luydkość jazdy f, , wynosiła 70 km/h O—r Możemy więc skorzystać ze wzoru (2.2>: piędkoŃO ta jest lówna ilorazowi pr/cmievvA.niu w czasie jawi) i czasu jazdy:

Av,

Al,

Przekształcając ten wzór i puKlaitiajai' dane. ulr/ymujcim tS.4 km)

A I,, = t). 12 h 4 0.5 li a 0.62 li iiid|Ktwicd/'

C) tle wynosiła twoja średnia prędkość < - w czasie, kloty upłynął od początku podroży, do chwili jwzyhyoa na stację Umzynową? Wyznacz ją na drodze obliczeń oraz grułiczr.ie

R0ZWIĄ2ANIE

O—* Skorzystamy znów ze wzoru (2 2) i\, JUi > alej/n>ttr/iżv jest niwna ilorazowi przemieszczenia wc:tiiietnlcj/lodrtJjy. równego 10.4 km. oraz czasu i oh j p/nlr<ii\, równego 0.62 h. Z równaniu (2.2) otrzymujemy więc;

t-i, -z — m    - lt>.8 km/h ś* 17 km/h. (odpowiedź)

M 0.62 h

Aby wy/niKzy\* c„ gr.iiic/me. sporządzimy najpierw wykres, jak na rysunku 2 > /.i/iuc/..jąe. żc nich odbywa się od początku układu współrzędnych do punktu oznaczonego jako ..'tacja". O—r Prędkość iicdma jest równa nachyleniu prosiej. l.-jeząccj le dwa punkty, czyli ilorazem roinicy ish rzfthtuh tAi = 10.4 km) i nifnrry u* tH/drnrbi Ar - 0.62 U), skąd otrzymujemy «•„ « 16.8 kni/li.

0.2

Rys 2.5. I*izykład 2.1. I Jdcinki o/iue/oHe tako .ja/da i „nursz s.i w y kresami z.iieżauiści położenia >il czasu dla czyści |Hxł*X*ży przebity di NuuocłKstcm i pieszo t/ułożono, że mas/emuałeś ze stała prędkością' N.ielw lenie |'rosiej. p«zceltod/ąecj prtc/ p«s.za-lek ukł.ulu wspoli /<dnyvh • punki oznaczony jako ..stacja jest nnuw średniej pplUKi dla całej psliozy. id jej |iv/.iikii ik* chwili j»rzybycia na stację benzynowa di Załóżmy. z.e nabrałeś benzyny dv» kanistra zapłaciłeś za ma i witkik-ś do samochodu w cztesic 45 minut Ile wynosi mcO-nu druga, pi zęby ta przez ciebie w jednostce e/asu. 'ił |xx /alkc |XMtróży do chwili powrotu / łvn/.yną J*» 1uigoivtki

?0IV/:aIamE.

Musimy obliczyć »l«»r.,z całkowitej przebytej przez cii hic drogi i całkowitego czasu jioilró/y. C ałkowita dme.i "yn«"i S.4. km ♦ 2 km + 2 km - 12.4 km. Całkowity c/as pndiwy jes niw ny. 0.12 h ♦ 0.5 h i 0.75 h = 1.37 h Ze w/om t2 *) "trzy imi|cmy więc:

02.4 km) ^V' “ (1.57 b)

9. t km/h.