32762 skanuj0052 (18)

84 B. Cieślar

Szukany promień przekroju będzie więc równy: r(x) =

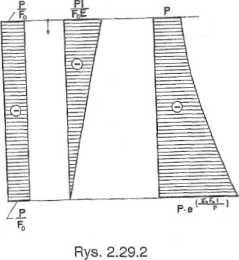
2.    Obliczenie naprężenia w dowolnym przekroju (rys. 2.29.2a)

°<*)#*Tt~***‘

3.    Obliczenie przesunięć punktów osi pręta

Przesunięcie u(x) punktu określonego współrzędną x jest równe skróceniu dolnej części kolumny, czyli odcinka zawartego pomiędzy przekrojem określonym współrzędną “X" a przekrojem określonym współrzędną x = I.

u(x) = Jedą =||d| = | jdą=2(1 - X) = hJjP - X).

Zatem:

u(0) = -^j-; u(l)= 0.

Łatwo zauważyć, iż poszczególne punkty przesuwają się w dół. Wykres przesunięć pokazano na rys. 2.29.2b.

Określenie funkcji siły osiowej:

N(x) = o(x)F(x)=-Pe“;

N(0) = - P;    N(0 = - P e⁰¹.

Wykres siły osiowej - rys. 2.29.2c.

[WM-l] Dla zadanego na rys. 2.30.2 układu statycznego i danych przed

2.30.

stawionych w tabeli na rys. 2.30.1, należy:

1.    sporządzić wykresy sił wewnętrznych;

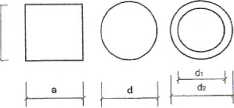
2.    zaprojektować przekroje poprzeczne prętów 1, 2 i 3 o kształcie, kolejno: kwadratowym, kołowym i pierścieniowym. Wymiary zaokrąglić do pełnych milimetrów;

3.    sprawdzić naprężenia w prętach;

4.    obliczyć całkowitą i jednostkową zmianę długości pręta 3 oraz jego całkowitą i jednostkową zmianę objętości.

Uwaga: w prętach ściskanych pominąć wpływ wyboczenia.

	..kN/m
=.......	...kN
=......	...m
_ _	....MPa
	....MPa
_	0
i/d2 = •

E = 2-10⁴MPa, v = 0,25

Dane: schemat nr

q

P

	sche mat	q	P	I	fdr	fdc	a	di/cfe
1	I	10	150	3	18	40	30	0,4
2	II	15	120	3,5	19	38	40	0,5
3	III	20	100	4	20	36	45	0,6
4	IV	25	80	4,5	21	34	50	0,7
5	V	30	60	5	22	32	60	0,8
6	VI	40	50	6	23	30	75	0,9

Rys. 2.30.1