15447 skanuj0051 (16)

82

B. Cieślar

Z równania (1) otrzymamy wtedy:

^RB = To^Fi^|-i^p-

Obliczamy wartości sił osiowych:

N.(0) = YoFil-fP:

Ni (I/4) = T«F$HfP|

Nn(l/4) = YoF^I+|P;

Ni. (I) =-Y₀Fil-}P.

Obliczenie niezbędnej wartości siły P, zapewniającej zerowe przesunięcie punktu C.

Warunek powyższy zostanie spełniony, gdy Al₍ = 0.

1/4

f^(R«-Y.Fz)dz = 0,

O

a stąd:

P = iY₀PI-

Wykres przemieszczeń punktów leżących na osi pręta pokazano na rys. 2.28.2C.

2.29.

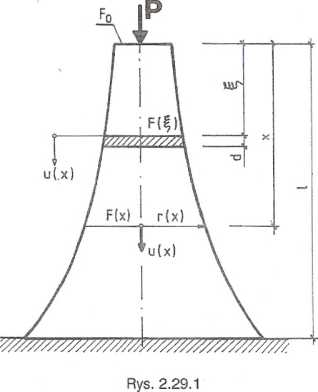
Wolno stojąca kolumna (rys. 2.29.1) jest obciążona na głowicy o polu F

siłą P oraz ciężarem własnym (y₀)- Należy tak dobrać zmianę promienia r(x) przekroju, aby w każdym przekroju kolumny naprężenia normalne miały taką samą wartość jak na górnej powierzchni kolumny. Następnie dla tak dobranego promienia przekroju sporządzić wykresy siły osiowej, naprężeń normalnych oraz przesunięć punktów leżących na osi pręta. Jako dane przyjąć: P, F,y₀ ■

Rozwiązanie

1. Określenie zmiany przekroju poprzecznego z warunku:

cr = const o = ^7-r = —(1)

r(X) r

gdzie: F(x) = 7t[r(x)]², a N(x) jest siłą osiową.

Siła osiowa w przekroju określonym współrzędną x:

(2)

N(x)=-P-jF(ą)Y₀dą.

Podstawiając (2) do (1) otrzymamy:

jF(S)Yo^dl

_P

F.’

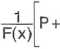
a stąd:

(3)

p+jFrav)ą=fF(x).

o    ^r»

Równanie (3) jest równaniem całkowym Volterry II rodzaju. Rozwiążemy go, tzn. wyznaczymy F(x) stosując rachunek operatorów [5].

Postać operatorowa równania (3) jest następująca:

P F(x) — + y«—-¹-s ^fo s

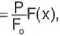
gdzie s - operator różniczkowy. Po przekształceniu mamy:

F(x)=F(x)=_i§_,gdziea=^,

a stąd postać nieoperaf<