53482 skanuj0117 (16)

214 B. Cieślar

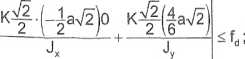
(2’)

Kś 0,01736 MNm.

5.8.4.2. Przekrój obciążony momentem ujemnym M₂ = 1,5 K.

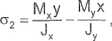
gdzie M_x = M_y = M V2/2 = 1,5K>/2/2.

Równanie linii obojętnej (o₂ = 0),

y = 2,143 x; tg(3₂ = 2,143;    |3₂ = 65⁰.

Położenie linii obojętnej jest takie samo, jak w przypadku obciążenia momentem Mi (por. 5.8.4.1). Wynika stąd, iż największe naprężenie wystąpi w tym samym punkcie przekroju co przy obciążeniu momentem M₂, czyli w punkcie II. A zatem

(3)

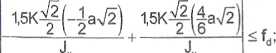
K< 0,01157 MNm.

Z warunków (1’), (2’) i (3’) wynika, iż dopuszczalna wartość parametru K jest równa 11,57 kNm.

5.9.£ Zaprojektować, z warunku nieprzekroczenia wytrzymałości obliczeniowej,

przekrój poprzeczny belki wspornikowej, pokazanej na rys. 5.9.1, jeżeli:

P = 30 kN, P = 20 kN, I = 1,2 m, f_d = 10 MPa.

Rozwiązanie

Przekrój poprzeczny belki przedstawiony na rys. 5.9.3 posiada cztery osie symetrii, a tym samym nieskończenie wiele par osi głównych, centralnych. Momenty bezwładności względem każdej z nich są równe:

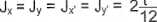
12 12

t⁴ , t(3t)³ ₌ 29_t4

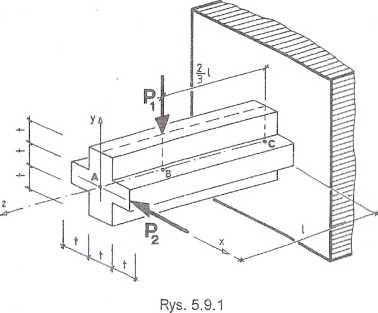
Wykresy momentów zginających, odniesione do osi x i y, pokazano na rys. 5.9.2b,c. Wektory tych momentów zaznaczono na rys. 5.9.3. W przekroju przy-podporowym (C) wartości momentów są sobie równe i wynoszą M_x = M_y = 24 kNm. Dodając wektorowo oba momenty otrzymujemy wektor wypadkowy M, leżący na osi głównej, centralnej y\ Przypadek ten możemy potraktować jako zginanie ukośne w układzie osi x,y (co byłoby wygodne, gdyby wektor M nie leżał na osi symetrii) lub jako zginanie proste w układzie osi x',y'. W tym ostatnim przypadku funkcja naprężeń ma postać:

a =

Mx' J, '

d)

gdzie:

M = 24 V2 kNm,

x' - współrzędna punktu w którym obliczamy naprężenie.

Linia obojętna w każdym przekroju poprzecznym belki - w tym przypadku - pokrywa się z kierunkiem wektora momentu zginającego. W przekroju przypodporowym największe naprężenia wystąpią w punktach I, II, III i IV. A zatem:

M • X m _< £ .

i ^di

24>/2 10-³ W2 ^_in.

29*4

12

tł 0,1257 m.