38247 P1080541 (2)

liczba wszystkich możliwych harmonik jest równa y. W szeregu czasowym oprócz wahań okresowych może występować stały poziom albo tendencja rozwojowa.

Przykład 1.16

Przewozy ładunków przez PKP w min ton w kwartałach lat 1995-1997 prezentuje tab. 1.21 oraz rys. 1.20. Na podstawie tych informacji należy oszacować harmoniki oraz sporządzić prognozę wielkości przewozów na cztery kwartały 1998 r.

Tabela 1 21

Wielkość przewozów ładunków przez PKP (w min ton)

Lata	1995				1996				1997
Kwartały	I	n	ffl	IV	I	n	m	IV	I	n	m	IV
__	54,6	54,6	58,6	59,6	iLŁ		56,2	S9J_	53,9	56,7	57,7	59.6

Źródło: „Biuletyn Statystyczny GUS”.

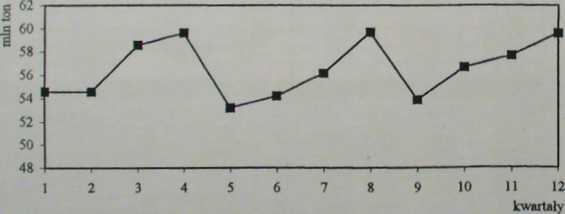
Rys. 1,20. Wielkość przewozów ładunków przez PKP w poszczególnych kwartałach lat 1995-1997

Rozwiązanie

Ocena wzrokowa wykresu wskazuje, że w szeregu występuje pewien stały poziom zjawiska i wahania sezonowe. Szereg czasowy zatem można przedstawić jako sumę harmonik:

gdzie: i - numer harmoniki,

A« - amplituda i-tej harmoniki,

et - przesunięcie fazowe i-tej harmoniki.

Korzystając z własności funkcji cosinus, można przekształcić rozważany model do postaci:

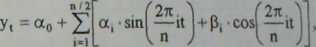
gdzie: eto, otł, pi - parametry.

Badaniem objęto n - 12 kwartałów. Liczba wszystkich możliwych harmonik zatem wynosi 6:

-    pierwsza harmonika ma okres 12 kwartałów, czyli 3 lata,

-    druga harmonika ma okres 12/2 “ 6 kwartałów, czyli 1,5 roku,

-    trzecia harmonika ma okres 12/3 = 4 kwartały, czyli 1 rok,

-    czwarta harmonika ma okres 12/4 - 3 kwartały,

-    piąta harmonika ma okres 12/5 - 2,4 kwartału,

-    szósta harmonika ma okres 12/6 ^m 2 kwartały, czyli pół roku.

Wartości parametrów oto, otj, P; szacuje się za pomocą klasycznej metody

najmniejszych kwadratów. Obliczenia związane z szacowaniem parametrów harmonik przedstawia tab. 1.22.

Stosuje się następujące wzory:

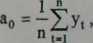
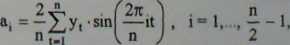
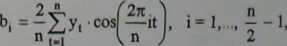
gdzie: ao, a,-, bj - odpowiednio oceny parametrów oto, oti, Pi. Dla ostatniej harmoniki o numerze — :

n w

Zatem: