013

13

1.2. Prawdopodobieństwo

Rozwiązanie.

Liczba wszystkich możliwych rozmieszczeń n kul w n komórkach jest równa n". Dokładnie jedna komórka jest pusta, jeżeli w dokładnie jednej komórce są dwie kule, a w pozostałych n — 2 jest po jednej kuli. Takich rozmieszczeń jest «(") (n - 2)!. Niech A oznacza, że dokładnie jedna komórka jest pusta. Ponieważ każde rozmieszczenie kul jest jednakowo prawdopodobne, to z klasycznej definicji prawdopodobieństwa otrzymujemy

Pr(A) =

n(")(n —2)! nⁿ

Przykład 1.2.4.

Z odcinka [0,1] wybrano losowo i niezależnie dwa punkty x i y, które dzielą ten odcinek ma trzy odcinki. Znaleźć prawdopodobieństwo, ze z tych. odcinków można zbudować trójkąt.

Rozwiązanie.

Wynik losowania można przedstawić jako jeden punkt (x,y) na kwadracie O. = [0,1] x [0,1], który przyjmujemy jako przestrzeń zdarzeń elementarnych.

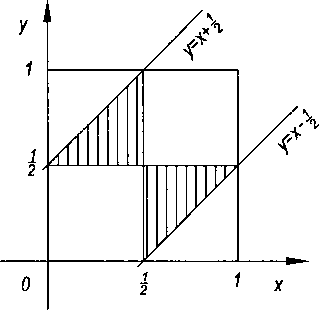
Rysunek 1:

Aby z odcinków można było zbudować trójkąt, każdy z nich musi być krótszy od sumy długości dwóch pozostałych, tzn. każdy z nich musi być krótszy od 1 /2. Zatem muszą być spełnione nierówności:

1 1 1

^x<r^y~^x<r^l~^y<r