35277 SNC03645

się względem siebie cząstki płynu (tj. gdy istnieje gradient prędkości), mają zdolnog wymiany pędu, która oznacza drobne zmiany gęstości strumienia płynu, a w komet wencji - zmiany wektora prędkości.

W atmosferze, szczególnie w jej warstwie tarciowej, gdzie kształtują się duże gradienty prędkości, turbulencja jest powszechną cechą ruchu. Wyjątkowo tylko, np. pod-czas ciszy, turbulencja zanika. Trzeba jednak podkreślić, że wielkość zaburzeń tuibo-lencyjnych odznacza się wielką amplitudą - obserwujemy różne nasilenie ruchów turbulencyjnych. Bezładne ruchy turbulencyjne sprawiają, że w atmosferze występują przepływy masy powietrza w kierunkach pionowych i poziomych. Oba rodzaje wymian masy różnią .się pod względem natężenia - poziome ruchy- uzyskują przewagę nad ni -nowymi nawet przy niezbyt silnym wietrze i pod względem skutków tennodynamin-nyeh. yakie urchqją mh pionowe. Z wymianą paommą wiążą się. jak już wiarą.

łdahiią™imim»^Tiimn ;m»yłnŁipM'liij pnrllfgjjaofyimranor.

rui -wAmt    - j----i—_m>.. pn

—*- ™    ■ ■ ■ rn-

f=*

a - gescś:    g -    u» i» 7i~evt.slt-fe w — prędkość ruchu pkmo-

>- JTUf~ — |ww»n. oraHir-nf r^m-

pcrmry y, - pwfc« adubUKan.

Enerpnazunwi iji a- napnknnaTifesiferig?tha5-i wyutj^ąeejzióżtńcgęstośdtnfe-ihy powietrzem unoszącym się i oziębiającym adiabatycznie a powietrzem otaczającym.

W mieszającej się turbulencyjnie atmosferze ruchy pionowe utrzymują się mimo I mc sprzyjających warunków termicznych - przy stabilnej stratyfikacji. Energia tych m- I chów pochodzi z energii kinetycznej ruchu poziomego, a przemiana energii zachodzi I dzięki pionowym różnicom prędkości wiatru. Gradient wiatru, jak wspomniano, wywo- I tuje zaburzenia ruchu poziomego, prowadzące do pionowych przemieszczeń porcji po- I wietrzą: jest to pionowa turbulencyjna wymiana masy A = kp, gdzie k - współczynnik turbulcncyjnoŚci.

Wzrost energii ruchów pionowych jest proprcjonalny do współczynnika pionowej wymiany masy A, pionowego gradientu prędkości wiatru duldz oraz aktualnej przewagi wymiany poziomej A, nad pionową A (ilorazu A,IA). Ponadto, przyrost energii wymiany pionowej zależy od cnctgii, potrzebnej do pokonania sity ciężkości, oddziałującej na poruszające się pówietf/.c, n ściślej ih) stosunku tej energii do wielkości pionowego gradientu prędkości wiatru, który - jak powiedzieliśmy - umożliwia przekształcenie ruchu poziomego w pionowy. Według I. Kojrccwlc/a (1959, s, 222) wzrost energii pionowych ruchów turbulencyjnych wyraża wzór ¹

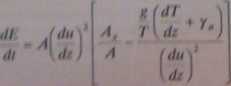
Przyrost energii, tzn. rozwój pionowej wymiany turbulencyjnej, zależy w pierwszym rzędzie od znaku i wartości bezwzględnej wyrażenia (glT)(dT/dz + yJKdu/di)¹. Iloraz len nosi nazwę liczby Richardsona. Można go zapisać w postaci

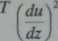
MIM

Widzimy, że liczba Richardsona jest wprost proporcjonalna do różnicy między gradientem adiabatycznym i pionowym gradientem temperatury w atmosferze, a odwrotnie proporcjonalna do temperatury bezwzględnej i kwadratu gradientu wiatru. Gdy liczba Richardsona Ri > A_Z!A, energia ruchów pionowych maleje (ponieważ dE/dt <

#) Jeśli natomiast Ri < A^łA, energia wzrasta (dEldt > 0).

Istnieją pewne problemy z określeniem krytycznej wartości liczby Richardsona, pen której Ri — A^iA. Chrgian (1969), za Lajchtmanem. podaje, że krytyczna wartość J6=0,2*). Wartość ta zależy od wysokości nad podłożem atmosfery. głównie dlatego, że aspókzynuk turfeulencyjności powietrza k zmienia aę znacznie w granicznej warstwie urnowej (współczynniki jest funkcją Ar). Dla swobodnej atmosfery przyjmuje się, że iczba Ri w granicach 05-4 nrmm slaby rozwój turbulencji. 05-OJD - umiarkowaną turbulencję, a Ri < 0 - silna turbulencję (Sobtśck. 1993, s. 64). Kształt krzywej, opisującej zależność energii ruchów pionowych od liczby Richardsona (zob. rys. SJ) pozwala także przyjąć, że ujemne liczby Ri odpowiadają rozwojowi turbulencyjnych ruchów pionowych, zaś dodatnie wartości Ri-oznaczają ich zanikanie.

Turbulencja ma istotne znaczenie dla pionowej równowagi powietrza, określającej — jak już mówiliśmy — warunki powstawania ruchów pionowych w atmosferze. Widzimy, że także turbulencja, czerpiąca energię z poziomego ruchu powietrza, przyczynia się do powstawania pionowej wymiany masy, nawet wówczas, gdy stratyfikacja termiczna jest stabilna. Liczba Richardsona wskazuje, że ruchy pionowe w atmosferze rozwijają się pod wpływem stratyfikacji termicznej oraz wskutek pionowego zróżnicowania prędkości wiatru.

Równowagę pionową atmosfery, kształtującą się pod wptywem tych dwu czynników nazywamy równowagą tenniczno-dynamiczną. Tak jak w przypadku równowagi termicznej, wyróżniamy jej stany chwiejne, stabilne i neutralne.

Kryterium identyfikacji stanu równowagi termiczno-dynamicznej można wyprowadzić z wzoru, określającego liczbę Richardsona. Jeśli przyjmiemy krytyczną wartość liczby Richardsona (Ri — 0,25), to kryterium stanu równowagi w powietrzu suchym stanowić będzie gradient temperatury, określony wzorem

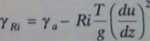
gdzie: Ri - krytyczna wartość liczby Richardsona, T - temperatura bezwzględna, g -przyspieszenie ziemskie, duldz - pionowy gradient prędkości wiatru.

Stan równowagi określamy, porównując gradient pionowy temperatury w atmosferze z wartością gradientu y^ w ten sam sposób, jak to czyniliśmy w poprzednich razach.

Pionowy gradient prędkości wiatru, jak również temperatura, przyczyniają się do obniżenia gradientu temperatury, przy którym obserwuje się chwiejność atmosfery, bowiem (y» ^< Ym)< jeśl* tylko prędkość wiatru zwiększa się z wysokością.

127

JmmtA

1

i iM,<lul4g pkmowy gzarllanl prędkości wiatru,