42495 Scan0050 (15)

że sytuacje zadaniowe występowały w toku większości zajęć praktycznych. Przedstawimy teraz fragment protokołu z obserwacji zajęć dydaktycznych, który charakteryzuje sytuację zadaniową wytworzoną podczas ćwiczeń z przedmiotu „Maszyny i napędy elektryczne”, przeprowadzonych ze słuchaczami III roku studiów..

Godz. 10,06. Nauczyciel akademicki W. H. — po podaniu uczącym się -tematu zajęć ćwiczeniowych: „Silniki bocznikowe prądu stałego” — oświadcza: „Na dzisiejszych zajęciach zajmiemy się rozwiązywaniem trzech ćwiczeń. Oto treść pierwszego ćwiczenia: „Silnik bocznikowy o mocy: P_n—30 kW; napięcie znamionowe: U_n = 220 V; natężenie prądu znamionowego: I_n=153 A; opór twornika: R_t= 0,11 Ohm; obroty znamionowe: n_ra=^!1000 obr./min — napędzając dźwigarkę podnoszącą ciężar — rozwija na wale moment: M=31,6 kG • m. Określić, z jaką prędkością będzie wirował silnik, jeżeli: a) w obwodzie wirnika nie ma oporu dodatkowego' (Ra)', b) w obwodzie wirnika jest opór dodatkowy (R_ci = l,6 Ohm). Przy wyliczeniach należy pominąć straty w przekładniach”.

Godz. 10,03. Nauczający poleca studentom przystąpić do rozwiązywania zadania. „Zadanie to — zaznacza — nie jest trud-ne. Podobnego typu zagadnienia już rozwiązywaliście. Pracujcie samodzielnie. A jeśli czegoś jeszcze nie rozumiecie, pytajcie, ja wam wyjaśnię”. Studenci przystępują do pracy. Jedni przeglądając notatki zastanawiają się, jak postępować przy rozwiązywaniu tego zagadnienia, inni przepisują z podręcznika niektóre dane do zeszytów, jeszcze inni — nie tracąc czasu — rozwiązują ćwiczenie w swoich zeszytach.

Godz. )10,12. Prowadzący ćwiczenie, przechodząc kolejno od stołu do stołu, obserwuje czynności słuchaczy. Student P. J. pokazując swoje notatki zapytuje, czy przyjęty przez niego- wzór na obroty silnika (n) jest właściwy. Nauczyciel akademicki po przejrzeniu jego notatek odpowiada: „W tym wzorze są błędy. Proszę przypomnieć sobie; przecież wzór na obroty silnika stosowaliśmy już na poprzednich zajęciach”. Student P. J. dziękując nauczycielowi akademickiemu przegląda notatki i podręczc-nik. Student E. Z. pokazuje swój wzór na obroty silnika. Jemu również prowadzący zajęcia poleca ponownie sprawdzić notatki i ustalić prawidłowy wzór. Jeszcze -kilku studentów zwraca się do niego z prośbą o przejrzenie, czy przyjęty przez nich wzór — za pomocą którego zamierzają określić, z jaką prędkością wirował silnik, jeżeli w obwodzie wirnika nie ma oporu dodatkowego— jest prawidłowy.

Godz. 10,15. Nauczyciel akademicki mówi do studentów: „Większość z was zastosowała prawidłowe wzory na obroty silnika. Niektórzy jednak podstawiają błędne wzory. Podam wam zatem wzór, na podstawie którego należy wykonywać obliczenia”. Pisze na tablicy:

Rt _

-¹ Godz. 10,16. Studenci rozwiązują zadanie dydaktyczne. Nauczyciel akademicki, przez cały czas chodząc po sali, przygląda-się ich czynnościom. Na sali panuje względna cisza.

Godz. 10,25. „Sądzę — mówi prowadzący ćwiczenie — że większość z was zadanie już wykonała. Kto chce podejść do tablicy i przedstawić pierwszą część zadania?” Zgłasza się student M. Z. Nauczyciel akademicki, pokazując przedstawiony uprzednio na tablicy wzór na obroty silnika, zapytuje studenta M. Z.: „Co teraz powinniśmy zrobić?” Rozwiązujący zadanie odpowiada: „Musimy obliczyć obroty idealne (n₀) i współczynniki (CŹ i C;,)”. Nauczający zgadza się i poleca wykonać obliczenia. Student M. Z. pod wzorem przedstawionym na tablicy pisze:

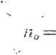
U„/i,    220-1000    220-10³

--------=--------- = ------= 1080 obr./min

R_t 220-153-0,11    203,3 7    '

W tym czasie nauczyciel akademicki zwraca się do studentów: „Proszę traktować wyniki obliczeń przedstawione przez kolegę M. Z. jako formę sprawdzenia prawidłowości waszych rozwiązań”.

Godz. 10,2;8. Student M. Z. kontynuuje rozwiązywanie zadania. Oto jego dalszy zapis na tablicy:

C'_E = — -----= 0,204

n₀ 1080

Ć^VM = 0,198

Cf Cm ⁼ 0,0-4-04

„Dane te — mówi student M. Z. — podstawiamy do wzoru na obroty silnika”. Pisze:

95