45458 Untitled Scanned 50 (2)

METRIA ANALITYCZNA

GEOMETRIA ANALITYCZNA

53

E

Zdający potrati

•    wyznaczać odległość dwóch punktów

•    wymucziu- odległość: punktu ud prostej, dwóch prostych równuleglych

S

3.9 n Dane są punkty /\ = (—2* — I > i /> = (!<», 4) oraz prosta k o równaniu y=-0,5.v+3. Oblicz

a) długość odcinka AB\ b) odległość punktu A od prostej l;:    c) odległość prostej k od prostej v --0,5.v + 2.

Zdający potrafi

•    graficznie przedstawiać równania i nli-r<iu mmi liniowe /. dwiema niewiadomymi

•    zaznae/ać w układzie współrzędnych zbiór punktów określony piv.cz układ nierówności liniowych

•    opisywać /a pomocą układu nierówności zbiory punktów

nik Chyl równy -6.

o rzędnej r. =3.

'(1,2);

3.10 Zaznacz w układzie współrzędnych zbiór tych punktów (v. y). których współrzędne spełniają warunek a) y=2v+3;    b) yS2r + 3:    c) y>2v+3.

3.11    Zaznacz w układzie współrzędnych zbiór A, jeżeli

a) zt={(.v,y): .v>() a v<0}; b) A = (U. y): ,v<2 a y> I }:    c) A = | (v, y): y^-.r-l a y£-.v+2j;

d) .4 = {(.v,y): .v+y-3<0 a 2t-y£0);    e) A = {U, y): ,t + v- 3<0 v 2v-v> ()}.

3.12    Opisz za pomocą układu nierówności zbiór punktów leżących między prostymi o równaniach y=2v i y=2v+3.

3.13 Opisz za pomocą układu nierówności zbiór punktów należących do trójkąta ABC. jeśli

a) 4=(0,0), Zł=(4,0). C=(0,4);    b) R 4 =((),()). B=(-A.O), C=(-2.-2).

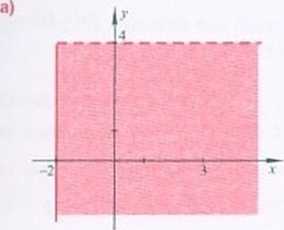
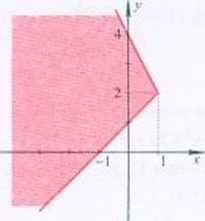
3.14 Zbiór, którego fragment pokazany jest na rysunku, jest zbiorem punktów płaszczyzny, których współrzędne spełniają pewien układ dwóch nierówności liniowych z dwiema niewiadomymi. Zapisz ten układ nierówności.

Zdający potrafi

wykonywać działania mi wektorach (dodawanie, odejmowanie, mnożenie prze/ liczbę) - u ujęciu analitycznym i syntetycznym

jeżeli prosta k ma

d) .v=-2.

jeżeli prosta k ma d) a--2.

b) Oblicz długość wektora AB. d) Oblicz, współrzędne środka odcinka AB. f) Znajdź równanie symetralncj odcinka AB.

3.15 Dane są wektory « = (-3.-2] i iv=[-l,4j. Oblicz współrzędne wektora i\ jeśli

a)R v=ii + »r,    b) v=-u:    c)R i"=5tr,    d) v =3w -4m:    e) v =2{:1 -3w)-u.

3.16 R Dane są punkty 4=(1, 3>. /? = (3. 7) i C=(5, 8). a) Oblicz współrzędne wektorów AB i BA. c) Znajdź taki punkt D, aby wektory AB i CD były równe, e) Znajdź taki punkt K, aby punkt fi był środkiem odcinka AK.

3.17 R Dwa punkty dzielą odcinek o końcach A = (17, 31) i li = (53, 58) na trzy równe części. Znajdź współrzędne tych punktów.

=0.