45956 str202

Rozwiązanie. Obliczań

ROZDZIAŁ 4

Równania różniczkowe cząstkowe rzędu drugiego

§ 1. Wiadomości ogólne

Definicja 1. Równaniem różniczkowym cząstkowym nazywamy równanie różniczkowe, w którym występuje funkcja niewiadoma dwóch lub więcej zmiennych i jej pochodne cząstkowe.

Definicja 2. Rzędem równania różniczkowego cząstkowego nazywamy najwyższy rząd pochodnej funkcji niewiadomej występującej w danym równaniu.

W tym rozdziale zajmiemy się równaniami różniczkowymi cząstkowymi rzędu drugiego, zatem równaniami następującej postaci:

(1.1)

*1 , X₂

du	du	d^2u	d^2u	d^2u
^xn > ^11 > ^ » • dx j	’’ dx„	’dx^2"	"’ź)x^2’	dx1dx

d²u \ Sx„-i dxj

= 0,

gdzie F jest funkcją wielu zmiennych określoną w pewnym obszarze wielowymiarowym. Definicja 3. Rozwiązaniem lub całką równania (1.1) nazywamy każdą taką funkcję

(1.2)    u = u(xi,x₂, ..., x„),

n zmiennych niezależnych x_t, x₂, ..., x„ mającą drugie pochodne w pewnym n wymiarowym obszarze fi, która po podstawieniu wraz ze swymi pochodnymi do wyrażenia F w zależności (1) spowoduje, że wyrażenie F będzie tożsamościowo równe zeru w obszarze fi.

Definicja 4. Zagadnieniem o warunku początkowym lub zagadnieniem Cauchy'ego nazywamy problem poszukiwania takiego rozwiązania «(x₁, x₂, ..., x„) równania (1), które dla pewnej wartości x_t = a_{ jest równe z góry zadanej funkcji <p(x₂, x₃, ..., x„) «— 1 zmiennych x₂, x₃,..., x„, tzn.

(1.3)    u(a₁,x₂,x₃, ..., x„) = ę>(x₂, x₃, ...,x„).

Zadania przykładowe

Zadanie 1.1. Sprawdzić, czy funkcja u = 3x³y—2y⁵ + 1 jest rozwiązaniem równania różniczkowego

d²u d²u „ 8u „ .

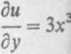
Wyznaczone pochodne pods skąd otrzymujemy

xi 118xy -2yu 9x²+x²(3x"

zatem funkcja u = 3x³y-2y Zadanie 1.2. Wyznaczyć

(1)

Rozwiązanie. Całkujerr jemy

(2)

gdzie (p(y) jest dowolną funk względem zmiennej y, skąd

(3)

gdzie F(y) = \ę{y)dy. Funkcj są dowolnymi funkcjami ról

Zadanie 1.3. Wyznaczyć

(1)

Rozwiązanie. Całkujerr następującą zależność:

(2)

gdzie ę{y) jest dowolną fun w dalszym toku przekształcei szego. Rozwiązujemy równan leży również od zmiennej x, funkcją zmiennej x. Rozwią;