str254

254 4. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE RZĘDU DRUGIEGO ( 8. ROZW

skąd po obliczeniu całek mamy

E„ =

8C/₀(—1)"⁺¹ n²(2n — l)² ‘

Obecnie możemy napisać w końcowej postaci funkcję u(x, t) opisującą drgania struny

.    . (2n —l)nx (2n-\)nvt

(—1) sin---cos---

(2n —1)

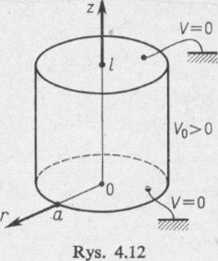
Zadanie 8.6. Wyznaczyć potencjał V(r, z) pola elektrostatycznego wytworzonego w walcu r<a i 0<z<l, jeżeli potencjał płaszczyzn z = 0 oraz z = / równa się zero, natomiast potencjał powierzchni bocznej walca r = a wynosi K_o>0 (rys. 4.12).

Rozwiązanie. Potencjał pola elektrostatycznego V(r, z) spełnia równanie Laplace’a

a2i

(i)

d²V 1

3+7

'dr²

dV d²V fr⁺~e?⁼⁰

który wobec założenia V„(r

Jeżeli R„(r) i Z„(z) są rc

^{(5) J} to funkcje V„(r, z) spełniaj?

(6)

Całkami ogólnymi równ

oraz następujące warunki brzegowe:

(2)    V(a,z)=V₀ dla 0 <z<l,

(3)    K(r, 0) = V(r, l) dla 0 Poszukujemy ciągu rozwiązań V_n(r, z) równania (1) w postaci

(⁴)    V_n{r,z) = R_n(r)Z_n(z).

Funkcje R_n(r) i Z„(z) dobieramy w ten sposób, ażeby funkcja V_n(r,z) spełniała równanie (1). Obliczamy zatem pochodne funkcji (4)

^ = KZ„

dr²

= K'z„

⁹ K

~dz² ~ ^R"^Zn

i podstawiamy je do równania (1) otrzymując stąd następujący związek:

1

gdzie I₀(x) jest zmodyfikoi K₀{x) — zmodyfikowaną fui Funkcja V(r, z) jest ogr zatem stałe B„ muszą być ze x = 0. Z warunków (3) otr

z„(0) = C,

Obecnie funkcję V(r,z)

(7)    .    1

gdzie E„ = A_nD_n. Funkcja ( czarny w ten sposób, ażeby

00

(8)    2]^

n= 1

Jeżeli do zależności (8)

(9)

to otrzymamy

(10)