str216

216 4. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE RZĘDU DRUGIEGO § 2. KI.AS

Po obliczeniu współczynników występujących w równaniu kanonicznym otrzymujemy

(4)

dtfr,

= 0.

Ogólnym rozwiązaniem równania kanonicznego (4) jest następująca funkcja:

(5)    utf,r,) = F(0+G(t,),

gdzie F i G są dowolnymi funkcjami różniczkowalnymi jednej zmiennej. Uwzględniając w zależności (5) związki (4), otrzymujemy ogólne rozwiązanie równania (1)

(6)

u(x, y) = F(y-x²+x)+G(y-x²-x).

Obecnie musimy znaleźć takie funkcje F i G, ażeby funkcja (6) spełniła dane warunki (2). Obliczamy w tym celu pochodną względem y funkcji (6) u(x, y)

^ = F'(y - x²+x) + G'(y-x² - x). dy

Z warunków (2) otrzymujemy następujące związki:

(7)    F(x)+G(-x) = (p(x),

(8)    F'(x) + G'(- x) = i/i (x).

Całkujemy obie strony zależności (8) względem * i wraz z zależnością (7) piszemy następujące dwa związki, w których nieznanymi są funkcje F i G:

F(x) + G(-jc) = (p(x) ,

F(x)—G(—x) = ji/r(t)dt.

a

Dodając lub odejmując stronami zależności (9), otrzymujemy nieznane funkcje

F(z) = ł(p(z)+ł$\j/(t)dt,

(9)

a stąd mamy

(10)

F(y-x²+x) = ł(p(y-x²+x)+$ J \l/(t)dt,

a

y — x²—x

G(y-x²-x) = ł<p(y-x²-x)-$ J il>(t)dt.

Uwzględniając wzory (10) w zależności (6), otrzymujemy szukaną funkcję u

y-x² + x

u(x,y) = ł[(p(y-x²+x) + (p(y-x²-x)~\+ł    J

Zadanie 2.8. Wyznaczyć

(1)

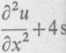
spełniające warunki

(2)

u(x,

Rozwiązanie. Daneró\ y+2<

są równaniami charakteryst; chodząc do zmiennych i

(3)    z = y

Po obliczeniu współczynnil

(4) ¹

Ogólnym rozwiązaniem róv

(5)

gdzie F i G są dowolnymi związki (4) w funkcji (5), c

(6)    u (x, y)

Obecnie należy wyznaczyć runki (2). Obliczamy w tyr

du

dy —

Z warunków (2) otrzymuje

(7)

(8)

Całkujemy obie strony i nością (7) dwa związki, w \

(9)

Dodając lub odejmując