33387 str234

234    4. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE RZĘDU DRUGIEGO

Własność 5. Rozwiązaniem równania fali płaskiej (5.14) spełniającym warunki początkowe

234    4. RÓWNANIA RÓŻNICZKOWE CZĄSTKOWE RZĘDU DRUGIEGO

(5.20)

jest funkcja

(5.21)

u(x,0) = (p(x)

(») ₌

’ W,-0

*(X)

X + Ct

u(x,t) = ł[(p(x-ct)+<p(x + cty]+^ j* \p (jj) drj.

x—ct

Wzór (5.21) nazywa się wzorem d’Alamberta. Zadania przykładowe

Zadanie 5.1. Wyznaczyć rozwiązanie równania fali płaskiej (5.14) spełniające następujące warunki początkowe:

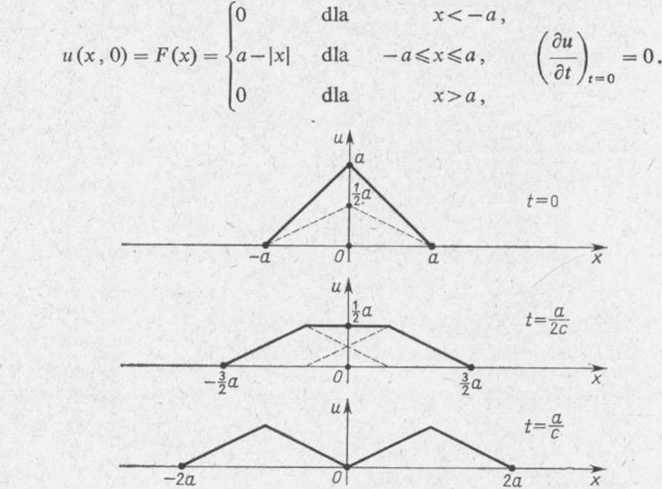
Rys. 4.9

Rozwiązanie. Zgodnie ze wzorem (5.21) rozwiązanie ma następującą postać (patrz rys. 4.9):

u(x,t) = £[F(jc—cO+F(x+cf)].