46412 str013

WiirloW impruwck At, Au, At'

Tablica i.i

...

I •

a =

D²

(1.47)

2(R + h_p)

Jeśli długość D łuku zawarta jesl w granicach 5 km < D ^ 10 km, zamiany takiej można dokonać, popełniając błąd nie większy od 8,2 mm.

Przykład

Długość I) luku na poziomie h_p = 500 m wynosi 8000,000 m. Korzystając z tablicy obliczyć długość stycznej, normalnej i cięciwy na poziomie h_p oraz na poziomie odniesienia (h_p = 0).

Dla I) = 8,0 km z tablicy odczytujemy

t = 4,2 mm, n = —2,1 mm, c= —0,5 mm;

będzie więc

T = D + At = 8000,0042 m N = D + An = 7999,9979 m C = D + Ac = 7999,9995 m

Rzut d łuku D na poziom zero obliczony ze wzoru

d = D (1 — -£) = 7999,3732 R

co już pozwala wykorzystać odszukane w tablicy poprawki do znalezienia t, n, c

t = d + AL = 7999,3774 n = d + An = 7999,3711 c = d + Ac = 7999,3727

I 1.4 (il I. li< >i. ns< ll<)RY/.ON TlI

prowadźmy przez punki centralny I płaszczyznę horyzontu i powierzchnię

.....a Ich ślady na przekroju normalnym reprezentują odpowiednio: prosta IV

lid kola IA długości D. Pion punktu K przebija te powierzchnie w punktach V,

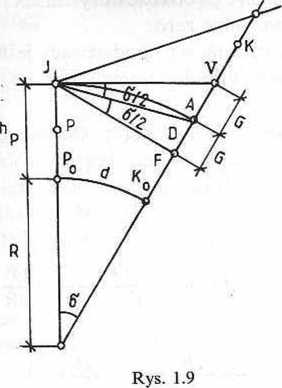
Wyprowadzimy wzór na długość G odcinka VA, reprezentującego odległość powierzchni horyzontu od płaszczyzny horyzonut, liczoną wzdłuż linii pionu punktu K (i nazwiemy głębokością horyzontu na poziomie h_p.

/ trójkąta IVA mamy

G = D|    (1.46)

n ponieważ ścisłą wartość kąta a wyraża wzór

D

R + h_n

Więc w wyniku podstawienia otrzymamy

G =

Wzór ten pozwala obliczyć poprawną wartość G głębokości horyzontu na podstawie długości łuku D na poziomie h_p.

Ponieważ

D = d(l +^)

więc podstawienie do (1.47) daje