47433 str124 125

Z uwagi na możliwość wyboczenia jętki trzeba także sprawdzić warunki jak dla elementów ściskanych — wg wzorów 4.2.1.i oraz j z PN-B-03150:2000:

'cOd

^cy fcOd    fmyd

^myd    ję ®mzd

<1,

mzd

'cOd

^cz fcOd

-+ k

o.

mzd

fmyd    f n

<1.

mzd

Analizując wzory 4.1.7.a,b oraz 4.2.1.i,j i biorąc pod uwagę, że moment zginający występuje w płaszczyźnie z-x, możemy stwierdzić, że najniekorzystniejsza wartości otrzymamy z obliczenia wg wzoru 4.2.1.i. Pominiemy zatem obliczenia ] przeprowadzone za pomocą pozostałych wzorów.

Założono przekrój jętki 2 (38x150)+ 50x38 mm (rys. 3-17a). Ściskanie z uwzględnieniem wyboczenia:

A_tot = 2-38-150+50 -38= 13300 mm²,

I_y = 2 • 38 • 150³/12 + 50 • 38712 = 21,604 • 10⁶ mm⁴, i_y = (/,M_ot)⁰'⁵ = (21,604-107 13 30O)^{0 5} = 40,30 mm, k_y = 2900/40,30 = 71,96.    ]

°_Ccńt = n²-^Eo,os/V = 3,14²- 8000/40,30² = 48,57 MPa,

7ei>> = (fcOk/Oc cri.)⁰’⁵ = (23/48,57)⁰-⁵ = 0,688>0,5,

k_y = 0,5[1 +^(A_rely-0,5)+A?_e!y] = 0,5[1 +0,2(0,688-0,5)+0,688²] = 0,755,    ,

Ky = l/[k,+(k²-A?_el/’^s] = 1 / [0,755 + (0,755² - 0,688²)^0,5] = 0,938, o_cQd = F_c0i/A_t o, = 6000/13 300 = 0,451 MPa, f_c0d = 23-0,8/1,3 = 14,15 MPa.

Zginanie:

M_yd = 0,125 • 1,33 - 2,90² • 0,9 = 1,2583 kN • m (moment zginający),

W_y = 2 • 38 • 150² / 6 = 285 • 10³ mm³, o„yd = Myj W_y = 1258,3 • 10³/(258 • 10³) = 4,877 MPa .

Dla belki usztywnionej na całej długości deskami pomostu k_crh = 1. W razie zniszczenia pomostu długość wyboczeniowa belki l_d - 2900 mm (tabl. 4.2.2 z ww. normy), a l_d/l_Tzecz = 1. Do wartości l_d należy dodać wartość 2h z uwagi na obciążenie belki górą. Smukłość sprowadzona

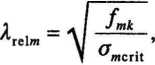
f_md = 30 -0,8/1,3 = 18,46 MPa.

= {(2900 + 2 150)150 18,46/

Udh-fmd	. 1^'Omean
V n b^2 Ek	V c i '“'mean

/ [3,14 • (2 • 38)² • 8000] • (12 000/750)⁰-⁵}⁰-⁵ = 0,494 < 75,

• Mlcm

l_tlll = 1,0 (wzory z p. 4.2.2.(3) z PN-B-03150:2000).

Sprawdzenie warunku 4.2.1.i z ww. normy 0.451/(0,938 -14,15) + 4,877/18,46+0 = 0,298<1,0.

t Sprawdzenie naprężeń przy uwzględnieniu wyboczenia w płaszczyźnie y-x (prostopadłej do szwów)

Sprawdzenie przeprowadza się wg wzoru 4.2.1 .j z ww. normy zmienionego f godnie z przypisem na dole str. 119 z tej książki do postaci:

/^,,"?-+^+V5^ai£l.

A., '/.O,/ fmyd    fmzd

% uwagi na jednakową wartość modułu E dla wszystkich składowych pręta, obllczumy:

M'¹ />ef ⁼ ^Omean ' hf'

= XIi+Y,2(A_ral),

1C /, = /, +/₂+/₃ = (2 • 150 • 38³ + 38 • 50³)/12 = 1767,63 • 10³ mm⁴,

X (A, aj) = 2 • 38 • 150[0,5(38 + 50)]² = 22,07 • 10⁶ mm⁴.

(hi obliczenia y_i potrzebny jest wzór 6.3.2.d z ww. normy

- 11 +7T²-E_i-A_i ■ sj(K_t ■ l²)]^-1.

(Mm obliczenia wartości K_i należy założyć średnicę i rozstaw gwoździ. Przyjęto gwoździe 4x 110 mm. Warunek z p. 7.4.1.(2) ww. normy został spełniony, gdyż

18/6>r/>38/ll, tzn. 6,3 mm>r/>3,45 mm.

Rozstaw gwoździ (zgodnie z p. 7.4.2.1 ww. normy): ii_ll()>x = 40d = 40-4 = 160 mm,

«,_mU = (5 + 5cosa)d = (5 + 5 -1)4 = 40 mm.

W obliczeniach występuje wartość s, definiowana w normie jako rozstaw Igeeników sprowadzony do rozstawu w jednej linii (osi) przekroju. Wartość s_min

125