TOB17
Sprawdzamy warunki początkowe dla t = 0+
iL(0+) = 7 - 5 = 2 A «c(0+) = 5 V
5.21. W obwodzie jak na rys. 5.21a w chwili t = 0 został zamknięty łącznik W. Metodą zmiennych stanu obliczyć prąd w cewce i napięcie na kondensatorze w stanie nieustalonym. Dane: E = 100 V; = R2 = R3 = 2 £2;
C = 0,5F;L = 2H;/? = in.
a) b)
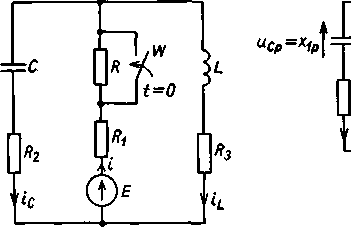
Rys. 5.21
Lcp
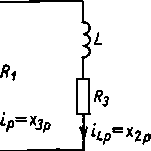
Rozwiązanie. Obliczamy prąd w cewce i napięcie na kondensatorze w stanie zerowym
id O") = id 0+) -
100
= 20 A
Mc(0 ) — Mc(0+) =
= 40 V
Obliczamy prąd w cewce i napięcie na kondensatorze w stanie ustalonym
lLu
E
Rl +
100
= 25 A
»c« = Riku = 50 V
Jako zmienne stanu wybieramy napięcie na kondensatorze i prąd cewki
*i(f) = «c(0
x2(0 = idt)
Tworzymy schemat dla składowych przejściowych (rys. 5.21b) i formułujemy równanie stanu dla składowych przejściowych. Prąd x3p na schemacie nie jest zmienną stanu. Zgodnie z prawami Kirchhoffa
uCp + R2 icp + Ri ip = O
+ Riip = O
R3iLp + LdlLp
d t
Stąd po uwzględnieniu przyjętych oznaczeń
x3p = C
dx
i p
d t
+ X2p
. dx,
, dxi
dx
dt , dx
dt
Po uporządkowaniu otrzymujemy
1
dt
*1 P =
Ri
(Rl + R2)CXlp (R1+R2)CX2p
2p (Ri + R2)L Równanie stanu ma postać
Ri v RiR2 + R3R3 + R2R3 Xlp (Ri + R2)L *2
1 Rt
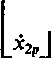
x2.
(R! + R2)C (Rt + R2) c
Ri Ri R2 + Rj + R2 i?3
(Ri + R2)L
L {Rt + R2)L
Zatem
det (A 1 — A) =
=u+i)(i+§)+
A =
|
2 |
2 |
1 |
- 1 | |
|
4 |
4-0,5 |
2 | ||
|
2 |
12 |
1 |
3 | |
|
L4-2 |
4-2 J |
. 4 |
2_ |
1
A2 + 2 A + 1 = 0; stąd = 12 = — 1 Macierz A ma podwójną wartość własną k{ 2 = — 1.
Wyszukiwarka
Podobne podstrony:
ScanImage003 (5) A. W obwodzie jak na rys. panował stan ustalony. W chwili t = 0 klucz został rozwar
75782 Skrypt PKM 1 00011 22 Zadanie 1.9 Dla produkcji jednostkowej układu łożyskowego, jak na rys. 1
Projekt MES Comsol Multiphysics 3.4 Rys. 21 Warunki początkowe dla pierwszej części łącznika 16
7 °lvtm 9, 9,2 kPa 31,5kN ■ m qrkm - 22,3 kPa 22,3 >9,2.2,02 Sprawdzenie warunku obliczeniowego d
BEZNA~16 Rozwiązanie. Warunki początkowe 1 Ai(o-)-,(°ł) = x
x = x0 + /40e p cos((«),/ + <p) Warunki początkowe (dla / = 0) II O II - XP = xo+Ao C0S(P -
Zdjęcie0454 Warunki początkowe. Dla t = 0■B j
Image36 70 a = g. v = V„ + gt, B»£ + 2 Warunki początkowe dla drugiej części ruchu znajdujemy podsta
Rozwiązanie* Warunki początkowe F 2 V ^° ) = i<0+) = 7^-2n-1 A uc(0-) - «c(0+) = R2 i (0) - 1 V S
50013 Image36 (14) 70 a = g, » = v„ + gt, x = . gt vot + -2 Warunki początkowe dla drugiej części ru
Obraz (2414) Warunki początkowe dla t=0 x = ay = ox = 0 y = VriC, = 0;C2 = a Fc3=-
więcej podobnych podstron