49642 skanuj0159 (14)

298 B. Cieślar

stąd:

h = _mi =m = ±^; _a = 54,74°,

czyli oś naprężenia 01 jest nachylona pod tym samym kątem w stosunku do dodatnich półosi x,y,z.

CT2 = - a;

(0 + a)l2 + a m₂ + a n₂ ^s 0; a l₂ + (0 + a)m₂ + a n₂ = 0; a l₂ + a m₂ + (0 + a)n₂ = 0;

O2)² + (m₂)² + (n₂)² = 1.

Identyczny układ równań otrzymamy dla o₃ = - a.

Ponieważ trzy pierwsze równania (podobnie jak w poprzednim przykładzie) są liniowo zależne, więc z fizycznego sensu wynika, że każda oś leżąca w płaszczyźnie prostopadłej do 01 jest osią naprężenia głównego <j₂ = a₃ = - a.

7.17. Dla zadanych składowych stanu naprężenia w punkcie (rys. 7.17.1) wyznaczyć wartości i kierunki naprężeń głównych.

Rozwiązanie

Porównując zwroty naprężeń przedstawione na rys. 7.17.1 z umownie dodatnimi zwrotami składowych stanu naprężenia otrzymujemy: o_x = 150 MPa, a_y = -30MPa, y, a_z = -20 MPa, txy = 20 MPa,

X)a ⁼ 40 MPa,    tyz = -60 MPa.

Wartości naprężeń głównych obliczamy z równania sekulamego: o³ - Si a² + S₂ a - S₃ = 0,

gdzie:

S₂ = -24500, S₃ = 0, 24500o = 0,

Si = 0,

o₂ ⁼ 0,

czyli: a³-a stąd:

d = 156,5248 MPa, c₃ = -156,5248 MPa.

VII. Stan naprężenia, stan odkształcenia__ 299

Wyznaczamy cosinusy kierunkowe osi naprężeń głównych.

<y 1 = 156,5246 MPa;

(150 - cti)Ii + 20mi + 40ni = 0;

20li + (-30 - Qi)mi - 60ni = 0;

40li - 60/11!+ (-120 - oi)ni = 0;

Óif+(mif + (nif = 1.

Stąd:

lt = ±0,9895, mi =±0,0646, n_t = ±0,1291.

Współrzędne dowolnego punktu (np. I na rys. 7.17.2), leżącego na prostej o kierunku naprężenia 01, który znajduje się w odległości n od początku układu współrzędnych, możemy obliczyć z zależności: Xi = Irh; yi = mi#| Z1 = firn. c72 = 0;

(150 - 02)12 ⁺ 20/T12 + 40n2 ⁼ 0;

20b + (-30 - 02)m₂ - 60n2 = 0;

40l₂ - 60m₂ + (-120 - o₂)n₂ = 0;

(l₂)² + (m₂)² + (n₂)² = 1.

Stąd:

l₂ = ± 0,00, m₂ = T 0,8944, n₂ = ± 0,4472.

G₃ = - 156,5248 MPa;

(150 - 03)13 + 20m₃+ 40n₃ = 0;

20b + (-30 - 03)m₃ - 60n₃ = 0;

40l₃ - 60m₃ + (-120 - o₃)n₃ = 0;

(fe)² + (ITI3)² + (f>3)² * 1-:ąd

l₃= + 0,1444, m₃ = ± 0,4425, n₃ = + 0,8851.

Kierunki naprężeń głównych pokazano na rys. 7.17.2.

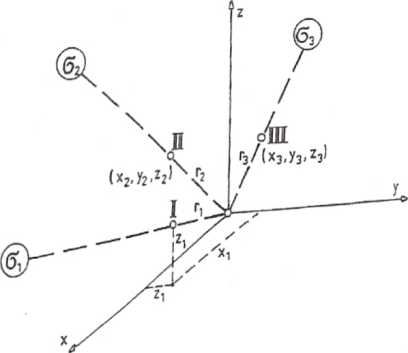
Rys. 7.17.2