56536 spektroskopia011

22

Jest to zasada zachowania wektora falowego (quasi-pędu) dla przejść optycznych w krysztale.

Ponieważ wielkość wektora falowego fali elektromagnetycznej 271

q = -j-« 10⁵ cm^-1 (w zakresie widzialnym) jest znacznie mniejsza od typowych średnich wartości wektora falowego elektronu, na brzegu strefy Brillouina k_mąr= - » 10⁸ cm^-1, wyrażenie (3.12) oznacza zachowanie wektora falowego elektronu w przejściach optycznych k_c = k_u. Przejścia takie nazwamy prostymi.

Przybliżenie to jest równoważne tzw. przybliżeniu dipolowemu,

0    którym mówimy wtedy, gdy długość fali znacznie przekracza rozmiar komórki elementarnej (porównajmy rozmiary: komórki — kilka A,

1    długość fali światła zielonego — 5000 A).

Dla małych wartości q możemy dokonać rozwinięcia w szereg Taylora

«*„+, = « k₀ + ‘l^v*^UTj_t„+ ••• •    (3-13)

Uwzględniając tylko wyraz rozwinięcia, otrzymujemy element macierzowy w postaci

|<c|e-p|y>|² = ( J u*k(e-p)u_{v k}dr)²,    (3.14)

^kel

znanej jako przybliżenie dipolem elektrycznym.

Jeżeli dipolowy element macierzowy jest równy zeru, to przejścia optyczne określane są przez    Teraz mamy

|<c|e-p|t;>|² = ( J q(V_Jtu*_k)(e • fi)u_uVdr)²    (3.15)

^kel

(całkowanie odbywa się dla komórki elementarnej k_el).

Wyrażenie to odpowiada przejściom elektrycznym kwadrupolowym lub magnetycznym dipolowym. Ten sam wynik otrzymujmy uwzględniając drugi człon w rozwinięciu A w szereg Taylora (i(q-r)). Przejścia kwadrupolowe są słabsze od dipolowych, w przybliżeniu jak kwadrat ilorazu stałej sieci i długości fali, a więc ok. 10⁶ razy.

Ograniczając się do przejść dipolowych, zauważamy, że k„ = k_t = k, a ponieważ element macierzowy pędu (3.13) słabo zależy od k, możemy napisać, wykorzystując (3.4),

l<c|H.,|»>² -    (3-16)

gdzie |PJ² - stała.

Prawdopodobieństwo absorpcji fotonu w jednostce czasu di otrzymamy podstawiając do złotej reguły Fermiego wyrażenie na element macierzowy (3.16)

(3.17)

= tZ I<^cl11>>|²<5(E_C(kj—E_v(kJ—hcó)

kc.k«

i dalej

9t{d) =

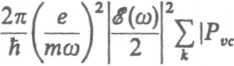
\²5(E_c(k)-E_v(k)-hc0).

(3.18)

Jeżeli sumowanie po wektorze k ograniczymy do dozwolonych w jednostce objętości, to wyrażeniu (3.18) odpowiada absorpcja fotonów o częstości cu w jednostce objętości. Strata energii pola w jednostce objętości wyraża się iloczynem dt i energii fotonu hen. Z drugiej strony zanik energii fali wchodzącej do ośrodka wyraża się przez

(3.19)

dl (dl\(dx\ c e₂al

gdzie a — współczynnik absorpcji, x — współrzędna opisująca wnikanie fali.

Gęstość energii fali I jest proporcjonalna do amplitudy pola elektrycznego

I = ^(a)\².    (3.20)

Wykorzystując równość —^ = dłhco, otrzymujemy

£₂M

a(£_e(k)-£„(k)-M

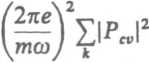
(3.21)

i analogicznie (np. stosując relacje Kramersa —Kroniga):

£ j((U) = 1 +

47ie^2 _1_	y	^f 2 ^N	\ l^l^2 1
m		K^mhc°evj	ICJ}^2v—(0^2

(3.22)