56763 str273

§ 1. POJĘCIE TENSORA 273

Wprowadzając te oznaczenia do wzorów (4) mamy

E„ =--sin0cos<p--sin0sinr/)--cos0,

dx    8y    8z

8v    8v    8v

E₀ =--q cos 6 cos cp —-— q cos 6 sin H--q sm 9,

8x    8y    8z

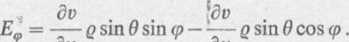
8x    8y

Zadania do rozwiązania

1.    W przestrzeni trójwymiarowej dane są równania ruchu x^r = x^r(t). Wykazać, że

dxT dxP .    .

zbiór wielkości A =--• — jest tensorem kontrawariantnym rzędu drugiego.

dt dt

2.    Wyznaczyć wyrażenia: a) SjA^, b) ó^sró^rs, gdzie 8^sr jest deltą Kroneckera.

3.    Dany jest tensor kontrawariantny rzędu pierwszego V^s =    , —, —| we współ

rzędnych kartezjańskich X³ = {x,y,z}. Wyznaczyć składowe V'^s tensora V^s we współrzędnych sferycznych x^,s — {g, 0,q>}.

. dx^r dx^a

4.    Dany jest tensor kontrawariantny rzędu drugiego V = — • — we współrzędnych

dt dt

kartezjańskich X³ = {x, y}. Wyznaczyć składowe V^,ks tensora V^ks we współrzędnych biegunowych x'^s = {r,(p).

zjańskich x^k = {x, y, z}. Wyznaczyć składowe A’_k tensora A_k we współrzędnych sferycznych x^,k = {q, 9,(p}.

6. Dany jest tensor mieszany A^k o Walencji dwa we współrzędnych cylindrycznych x* = {r,cp,z}. Wyznaczyć składowe A\^k danego tensora we współrzędnych sferycznych

x'* = {(?, 0,cp}.

7. Obliczyć wyrażenie A_klx!^cx^l w przestrzeni trójwymiarowej.

Odpowiedzi

1. A'^mn = A^u

8x^,m 8x^,n

8x^k' 8x‘ ‘

2. a) A_rm, b) 3.

3. V'¹

dx

~dt

sin 0 cos <p+-j- sin 0 sin <p +

— cos 0, dt

18 —Wybrane działy matematyki...