64441 P1010765 (2)

162

3. FUNDAMENTY

Rozpatrując składową silę dZ równoległą np. do osi y otrzymamy

. Nr cos 0 . . Ny . . dZ,—dZco*8—    • dxdy=-r—dxdy.

I

O hn    O hn

+W2    +W2

r . r Nydy N

" J ^X J b²h„ b^zh_D -1/2 0

Zatem całkowita sita tego kierunku działająca na całej szerokości stopy wyrazi się wzorem +wz +wa

(3-1)

y²J**'*._ Nb* ^N(b-aJ

^■■■■■

Z podobieństwa trójkątów rys. 3.1 otrzymano

b _ b—a, ho hę

Na podstawie doświadczeń stwierdzono, te w stopach tych ścinania i przebicia motna nie sprawdzań. Jeżeli tylko nie są przekroczone naprężenia przyczepności a średnicę wkła-

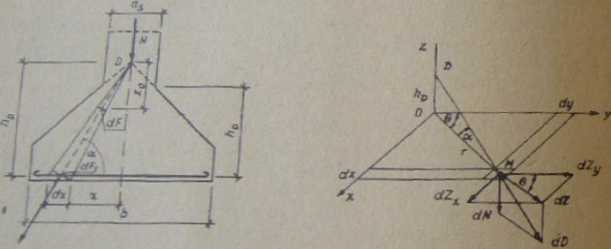
Ry*. 3.1. Schemat działania sil w stopie funda- Rys. 3.2. Wektory sił w elementarnym wycinku meatowej    podstawy stopy fundamentowej

dek należy tak przyjąć, by nie zostało przekroczone naprężenie dopuszczalne. Sita przyczepności na jednostkę długości prętów zbrojenia będzie

m

dZ,_ Ny dx b³kp

dla j~bfl mamy na krawędzi stopy

dZ,_N(b-a_M) dx    2 b%

Po scalkowaniu tego równania i podstawieniu odpowiednich wartości otrzymamy wzór na obliczenie naprężeń przyczepności

(3.2)

N(b-aJ °'⁼2bⁱh₀U *

).I. WYMIAROWANIE STÓP FUNDAMENTOWYCH

163

przy czym (/jest sumą obwodów prętów w stopie na jednostkę szerokości. Doświadczenia wykazały, że gdy pręty są zakończone hakami i rozstaw ioh nie przekracza jednej czwartej wysokości użytecznej stopy, można obliczenie przyczepności pominąć. Stopy prostokątne, obciążone osiowo, można obliczać analogicznie do kwadratowych, z tym 4e dla kierunku X i y oblicza się osobno zbrojenie i naprężenia przyczepności. Wzory zatem przybierają postać

N(b,-a„)    N(t.₂-aJ

¹    8h₀    ’    gh, ’

(3.3)

*(ł>t-a„)    N(b₂~o,J .

2b₁h„V_l ’    2b₂h₀U₂ '

gdzie U, i (/₂ oznaczają sumę obwodów wszystkich prętów równoległych na całej szerokości stopy odpowiednio do boków 6₂ i b₂.

3.2.2. Stopy obciążone mlmośrodowo

Przedmiotem rozważania są stopy, których środek ciężkości podstawy pokrywa się z osią słupa przekazującego na stopę obciążenie N i M. Rozpatrzono tu dwa przypadki:

1)    gdy położenie siły osiowej określonej mimośrodem e= MIN jest w granicach rdzenia podstawy,

2)    gdy ta siła znajduje się poza rdzeniem.

Rys. 3.3. Rozkład naprężeń w przekroju słupa i płasz-czyźnie stopy

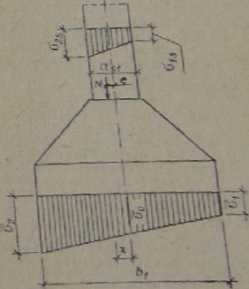
C3.4)

Przyjęto również założenie, że rozkład naprężeń w płaszczyźnie stepy jest taki sam jak w przekroju słupa,

Przypadek I

M b

Przyjmując pojęcie mimośrodu względnego k=e/b i opierając się na trapezowym rozkładzie naprężeń, otrzymujemy wzór na moment gnący w przedziale 0<:t<0,5 a_M po