66851 skryptA

Cyfrowa filtracja adaptacyjna s^en^aów czasowych Estymacja i ączma sk.oreiowamych szf.regów czasowych

164

(6.128)

Rckurencyjne (i ortogonalne) rozwiązanie postawionego problemu wynika z interpretacji unormowanych błędów prognozy w tyl (6.43) jako bazy ortonormal ncj podprzcstrzeni So,„j- W istocie, z (6.42) i (6.43) wynika. Ze

K >T

6 So.n.T

X óo,„-i_;r skąd wniosek, że óo,/..r = -So,,i-i;r®s/>an{kn >r}

(6.129)

(6.130)

Rozważając (6.130) dla n = 0,    ..N otrzymujemy ortogonalna dekompozycję

przestrzeni estymacyjnej So.nj jako

So.n.t = ®n-o^sP^an{\^r” >t)    (6.131)

Stąd wniosek, że

{lo)>ri|fi    }    (6 132)

stanowią elementy bazy ortogonalnej przestrzeni estymacyjnej. Zatem mamy

^p(So.n.t) - X >ż)

n=0

(6.133)

Cyfrowa filtracja adaptacyjna szeregów czasowych wynikającą z. (6.130). otrzymujemy

K >T = (I- P(So.n;T)\x >T= I-¹ >T ~^P(So.nj)\x >T ~ ^P{\^rn >t)\* >T =

= K-_l>T-\rn>T<Tn\x>T    (6 142)

Zauważając, że |r„ >7- X P(So._n-i.r)l-* >76 So.„- 1.7 oraz wykorzystując (6 140) , z n zamienionym na n - I. iloczyn skalamy < r„|x >_T możemy przepisać jako

< t„\x >r = < r„|(|x>_r -P(So,„-\ j)\x >r) =< r„K_, >7=

J-

= < r„|ej_| >_r<    >f=

= Pi.T <    >T

gdzie zdefiniowaliśmy

Pn-.T=< óK-, >T

Z połączenia (6.143), (6.140) oraz (6.142) wynika, że K >T= |k-| >Z -\r„ >T P„V] < tf-lK-l >7 <    >7'

(6.143)    ^: ~

‘ XV .

(6.144)

(6.145)

Wykorzystując tożsamość < e'|ej >r= I. otrzymujemy ostateczną postać unor-mowaną poszukiwanego rozwiązania rekurencyjnego

l^>r=(|ej-_l >r >r PńVl[l - (Pńr)²]^_i    (6.146)

Stąd

< *|ej >_r= [< n\e\__x >T - < n\r_n >7 P„'_;rJ[l - (p„V)³]'^j    (6.147)

i w końcu

^_jj. = [l-(p'7.)b-i^_,;r_r_nirp;.₇.]    (6.148)

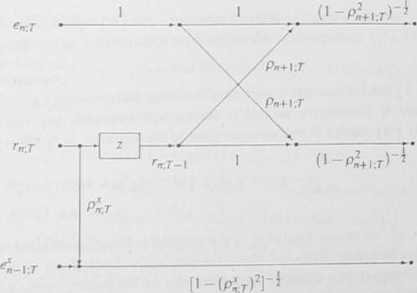
Zależność powyższa umożliwia ortogonalną realizację unormowanej sekcji (ii tru estymacyjnego Wykorzystując w tym celu (6.54) i (6.55) z 11 + I zamienionym na n, otrzymujemy (dla n = 0.....N) graf przepływowy tej sekcji, przed

stawiony na rys. 6.18 lnicjalizację (dla n = 0) w dolnej gałęzi tej sekcji stanowi próbka r' _1;(. Możemy ją wyznaczyć, rozważając

K1 >r= Ki >t< diKi >,

I

(6.149)

gdzie

^p(\^r« >t) = |r„ >r< r„|_{r    (6 n4)}

Wykorzystując (6.I34) w (6.I26). otrzymujemy rozwiniecie ortogonalne es.y-

ITlaLOrrl    y

>T~ £|r„ >T< (n\x >r

n=0

(6.135)

baz^PY°ON    ^C7ęf°^{WeJ S7erC8U F0UriCra elemen,U} I' >r ^wzg'ędem

oazy UN (|r„ >r}_n__n podprzestrzem estymacyjnej. ze współczynnikami Fouriera < r„|x>_T Wówczas z (6.126) i (6.127) wynika, że

II \t-Ń >t II' = < a£|£& >_r=< sj|(|x>z -|i_w >_r) =< ej|x>_r>,.=

= (< -*la < *At|r)|-r >r=< x|x >_T - < i„|x >_r=

= II \^x >T II³ ~ Yj < ^r»l* >r    (6.136)

n=0

i jeśli || |e^f >r II —*• 0 dla N —y co, to otrzymujemy równość Parsevala

|||x>7- |i =^<r„|x>j-    (6.137)

gdzie { < r„|x >_r }”₌₀ stanowi poszukiwaną ortogonalną reprezentacje elementu |x >_T w podprzestrzeni So.n j

Rckurencyjne rozwiązanie rozważanego problemu można łatwo otrzymać dzięki wprowadzeniu błędu estymacji rzędu n

K >r= ^p{S^,o.t)\^x>t=\x>t -P(S,,.o:ż)I*>t    (6.138)

wraz z jego wersją unormowaną

K >r= K >r<    > j '    (6 139)

implikującą zależność

K >T= K >_T<    >t    (6.140)

Wykorzystując w (6 138) dekompozycję operatora projekcji ortogonalnej

P(So.nj) = P(Sl).n-l.r) +P( Wn >t)    (6.141)

165

Estymacja i/jczna skorelowanych szeregów czasowych

<<r-u_:r

Zn + I: ż

Rys. 6.18. Sekcja filtru estymacyjnego działającego na próbkach Ponieważ z (6.138) otrzymujemy Ki >r= \x>t- [to- -tr]' zatem

< eliKi >r~< 4^t>r= f Z = °f

>_r=|x>r(«?)-' = [J-5] ^=N •^Xrl'

gdzie
A	XT_
*7 =	°T
Stąd
eii.T	= *r

(6.150)

(6.151)

(6.152)

(6.153)

(6.154)

Na tej podstawie otrzymujemy sek^ę untąah^jącą^hm-JToJo*'^^^^.^ _nQr.

lub schematycznie na rys. 6.20, gdzie przez ₀

malizacji

^ = [l-(p₀V)^,rⁱ • « = 0... .A'-!

(6.155)

167

166