15904 skrypt6

CYFROWA FILTRACJA A DAR IACYJNA SZEREGÓW CZASOWYCH _Adaptacyjna parametryzacja onToooNAcMA szEncmy,, _02ASOWV

gdzie inicjnlizacja wynika z (6.64), zaś

©W:r = QnjQn-\.t ■ ■ 0\.T    (6 66)

stanowi globalną realizację ./-ortogonalna filtru.

6.3.2. Uaktualnianie w czasie parametrów filtru

Dotychczasowe rozważania umożliwiają realizację /-ortogonalnego filtru para-metryzującego obserwowany szereg czasowy. Jak widać z rvs. 6.5 - 6.7, sygnałem wejściowym filtru są kolejne unormowane próbki tego szeregu W filtrze są przetwarzane jedynie odpowiednie próbki sygnałów błędów w przód i w tył w poszczególnych sekcjach filtru. Dlatego też można by sądzić, ze przedstawiony algorytm parametryzacji szeregów czasowych nadaje się do implementacji w czasie rzeczywistym. Niestety, przeszkodę stanowi wynikająca z Twierdzenia 6.1 metoda estymacji parametrów (tj. zależnych od czasu współczynników Schura) filtru Zgodnie z (6.49). współczynniki te wyrażają się jako

p„+i_;r = < e„\zr„ >r= -[«n:0 e„-.i ■ ■ ■ e„j][0 r„,o ■ ■ ■ 'Tt.r-i] =

= -2>„z6.z-,    <⁶⁶⁷>

(=0

Zatem z (6.49) wynika, że do wyznaczenia współczynników Schura p„₊i.r, 7 = 0.1,2,... w kolejnych sekcjach filtru (tj.. dla » = 0, .N - I). niezbędne byłoby przechowywanie w pamięci próbek sygnałów [e_n0,. i {r„o,- ■ •, r„T-1} dla 7 = 0,1,2,. .. co z oczywistych powodów stawiałoby pod znakiem zapytania możliwość realizacji filtru parametryzująccgo w czasie rzeczywistym (nawet w przypadku realizacji wieloproccsowej) Dlatego tez celowe staje się rozważenie możliwości rekurencyjnego uaktualniania w czasie parametrów filtru (co sugeruje zależność (6.67)) Idea takiego uaktualniania w czasie współczynników Schura polegałaby na wyznaczaniu ich w chwili 7 na podstawie wyznaczonej uprzednio wartości w chwili 7 - I. z uwzględnieniem poprawki wynikającej z obserwacji próbek e„ _T oraz r„ _T ,. tj. wyznaczania ich w sposób rekurencyjny jako

Pn+\:T ~ Pn+l:T~\ + poprawka    (6.6S)

Najprostsze wydaje się wykorzystanie w tym celu zależności (6.67). umożliwiającej -jak można sądzić - dekompozycję

< e„|zr„ >y=< e„\zr_n >r-i +e_njr„.T-i    (6 69)

W tym celu rozważmy

|e_n >T = |c_n >T< E„\e„ >t =

-    ^{< £}"l^e" ^>J '    ^S".7-1 < ^E"l^£" >r^ ^F-n.T <    >^]    (6.70)

gdzie

< £n\£n >T — < e„\r.„ >T-l +E²_;j-    (6.71)

Jednocześnie zauważmy, że

|e„ >r-t = |c_n >t-i< e„\e„ >t-\-

— [^En;0 < E„\e„    | ... E*;7-_ | < E„\e„ >7^ \ 0 ] =

⁼    ••««,T-|0]    (6.72)

skąd wniosek, że niestety

kn>r= \e„>t(< e„\e„ >r-t +4r)~* ź\e_n>_T-\ +[0 ...0e„_;7]    (6.73)

Z tycłi samych powodów

I-r„ >_T = |v„ >_T (< v„|v„ >_T_, -ł-v^_:7-_,)-i yś

jć |zr„ >_r_| +[0 ... 0r„._r_, ]    (6.74)

Rozwiązanie uaktualniania w czasie współczynników Schura umożliwia wykorzystanie tzw. „operatora różnicowego" [35] postaci

V    < ż|y >_T=< z|y >r - < -r|y >r-t ’    (6.75)

który w interesującym nas przypadku wyraża się jako

V    < »|/^,(Sf;„_;r)l^l’>r=

=< «|P(Sf;„_;7-)k >_r< rr|P(S^._r)|u >< zr|P(S^„_:7-)lzc >₇‘    (6.76)

dla dowolnych |u >7 i |u >7■ € Mt Wprowadźmy tzw. „normalizację informacyjną” [35) wektorów błędów w przód

|e„ >r—    >T<    >_T\

i w tyl

|:r„ >7-= |r„ >t<    ⁿ >t

(677)

-i

144

(CMIBBEEESBBBBllll

CYFROWA Fil TRAĆ. 1A AnAPTAOY.IMA SrPnPnAtfl r7AQOUUVrn    Tr

Adaptacyjna parametryzacja ortogonalna szeregów czasowych

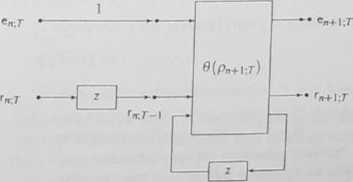
Rys. 6.9. Schematyczna reprezentacja sekcji 9(p_n+i;r) filtru adaptacyjnego

Cyprowa filtracja adaptacyjna szeregów czasowych Wówczas mamy

Pn+I;T = Pn+|;7-|( I — e²j-) - (1 - r²._r_,)^ + e„_:7-r„ 7_|    (6.79)

Wzór (6.79) określa poszukiwaną zależność rekurencyjną uaktualniania w czasie współczynników .Schura. Uzupełniają go poniższe „podwójnie” unormowane zależności na podwyższanie rzędu estymatorów w przód

e<i+l;ż = (1 -P„²+I;r)-*(1 -'l.T-\)~h^en;T + Pn+\jrn.T-l]    (6 80) |§f

i w tyl

^rn+l_;r= (1-p²+|_;7-) ł(l —    ^ [A>+l;7*B.r + ^tniT-11    (6.81) Jji

Zależności rekurencyjne (6.79)-(6.8l) umożliwiają realizację sekcji /-ortogo-nalnego adaptacyjnego filtru parametryzująccgo Wprowadzając oznaczenia

= (l-p„²+i_;T)-i

^E« = 0 -ś&rH    (6.82) ~

= (• ~^rij-1)^-^

w celu zwartości zapisu, zaleZność (6.79) przepiszemy jako Pn+l-.r = p„+\ j-[E~'-e„_;rr„.r-.t    (6.83)

Wzory (6.80)-(6.8l) możemy zapisać wówczas łącznie w postaci macierzowej

^e«-n;r		Rn 0	Nn+] 0	^1 Pn+llż	' 1 0	^e";7-
. ^rn+l;ż		.0 E„	.0 w„+l	.Pn+llT 1	0 z	.^TnJ .

(6.84)

Sekcję adaptacyjnego filtru innowacyjnego przedstawia rys. 6.8, którą można schematycznie przedstawić na rys. 6.9 lub - analogicznie do (6.56) i rys. 6.4 -jako sekcję z rys. 6.10. Realizację kaskadową adaptacyjnego filtru parametry-zującego przedstawiono schematycznie na rys. 6.1 I Jak widać, w algorytmie adaptacyjnej filtracji innowacyjnej wystarczające jest wykorzystanie jedynie dwóch elementów pamięci na sekcję (przechowujących, odpowiednio, wartości r„_;r-1 oraz. p„₊|._r_|). Dzięki temu jest możliwa realizacja filtracji adaptacyjnej szeregów czasowych w czasie rzeczywistym (z wykorzystaniem przetwarzania równoległego i potokowego). Przetwarzanie równolegle wynika z możliwości zastosowania N procesorów, z których każdy realizowałby operacje przedsta-

wionę na rys 6.8. W celu zapewnienia przetwarzania potokowego byłoby niezbędne, aby wszystkie operacje przedstawione na wymienionym rysunku były wykonywane w czasie krótszym od odstępu próbkowania obserwowanego sygnału.

Z rozważań przeprowadzonych w niniejszym punkere wynto te zaJe^tóc. (6 79M6.S4). w połączeniu z rys. 6.8 -6.11. umożliwiają rea izację cyfrcwego filtru parametry żującego obserwowany szereg czasowy, z możl.wośctą przetwa-

147

146