51838 skrypt7

_A0_APTACYJNA PAPAMĘinYZACJA ORTOGONALNA    ^

Cyfrowa filtracja adaptacyjna szeregów czasowych

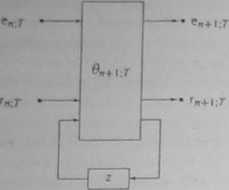
Rys. 6.10 Sekcja ft,₄, r Hltru adaptacyjnego

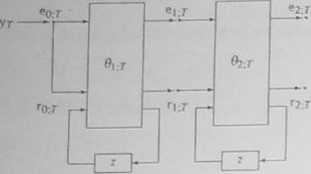
RYS. 6.11- Realizacja kaskadowa adaptacyjnego filtru parametry żującego

*r.T tv- i.r

v-l .7
		&S':T
-\.T

e^r

^r-vr

L-m*-¹

ramia równoległego i potokowego Jest to więc realizacja ukierunkowana na przetwarzanie w czasie rzeczywistym, a zatem mająca istotne znaczenie prnk tyczne. Jedyne co pozostaje - to przyjęcie właściwych inicjalizacji w algoryt mie adaptacyjnej parametryzacji szeregów czasowych Choć jest to - dc facto -zagadnienie elementarne, to celowe jest jego hardziej szczegółowe przedysku towanie. Problemowi temu został poświęcony kolejny punkt

6.3.3. Inicjalizacje i przykład działania filtru

Przypomnijmy, żc danymi wejściowymi algorytmu są próbki oImta uwaneeo lewostronnie okienkowanego y_, = 0 , f = 1.2... szeregu czasowego Interpre tując parametr T = 0,1,.. jako czas bieżący, na w stepie rozw azy my działanie algorytmu filtru paramctryzującego na przykładzie, prezentują jawnie / >: • ści (6.79)-(6.81) dla początkowych wartości 7 - 0. 1.2 oraz n 1.2.31 'moż Iiwi to przedyskutowanie działania filtni oraz przyjęcie poprawnych miciahznui w jego implementacji.

148

tiul

*7 = 0

Ijaic jalizac ja alqorvtmvi:

♦    próbka obserwowana: yo

♦    estymacja wariancji: C₀ = G+yJ; = C₀^{1 2}

♦    próbka unormowana: y₀ = ~

Komentar² c jes, małą sta!,, dodatnią, eliminującą przypadek dzieleń,a ^p .ero przy wyliczaniu próbki unormowanej y₀. gdy vo = 0 rn nn

7ab ^Za '1^bą I Z °, °^C2y"'^LUe' ^{ie w}P^ty'^v “j orbitalnie przyjętej stałej .antka po kilku lub kilkunastu krokach.

♦    inicjalizacje sygnałów: e_0;0 = r_0;0 = y₀

Stąd i z faktu, iż y_, = 0 wynika, że r_n._, = 0 , n = 0.....N - \

♦    inicjalizacje współczynników: p„._, = o, n= 1, ,N

- Algorytm:

♦    sekcjan= 1 ((6 79)-(6.81)dla 7‘ = 0orazn = 0):

Pi.o — Pr_j (l - €q.q) ! (l — rQ._,) ł — eo_;oro_;_| =

= 0(1- ej-o)) ■ l - eo.o 0 = 0    (6.85)

^ i .o = (1 - Pro) ł (l - T0. _ |) ~! (eo# -f pi ,oro_;- il =

= ¹ • I [«o# + 0 • 0] = eo#    (6.86)

^r t # = (I - pf#) - (1 ~ eQ.₀) “ ł [pi .0²0.0 + fo-.-1] =

^{= 2} ‘ 0 “ ^eo.o)’ ² [0 ^eo.o +0] = 0    (6.87)

♦    sekcja n = 2 ((6.79)-(6 81) dla T = 0 oraz n= 1):

P2# = P2.-i(l — e?₀)i(I -r?._,)ł -e,_;0r,_;_, =

= °0    •¹ — e I ;0 ² 0 = 0    (6.88)

^e2;0 = (l-p2;o) ■ 0 ~ ^rl.-l)”^[^el.0-bp2.0f0;-l] =

⁼ I l[^ei;0 + 0 0] = ei o= eo.o    (6.89)

^r2;0 = (1 “ P2#) ^0 ^_el;0)~^(P2.0e|;0 + r| _|] =

= l (l-e^H[0 ei_;o + ₀] = ₀    (6.90)

149

__Adaptacyjna parametryzacja ortogonalna szeregów czasowych

^eW ⁼ 0 ~Pu)~^(ł -^ro.-o) ^[^eo.i +Pi;ir(ho]    (6.93)

^rl_;l=(l-PM)^_l(I-4.l)"²[Pl;l^eO;l+rfto]    (6.94)

Jak widać, sekcja n = I, począwszy od chwili T = I. działa z niezerowymi wartościami początkowymi, dając na wyjściu niezerowe wartości.

« sekcja n = 2 ((6.79)-(6.81) dla T = I oraz n = 1):

P2;l = P2.(][ 1 — «f;t) ^ (l ^{— r}f;o) ^ -«l.t^rl;0 =

= 0 (1 — ef.,)ł I-e_u 0 = 0    (6.95)

^e2.l = (I-P2.l)'^(l-r?_;oH[^eW+P2;l^rl:o] =

= 1 lfe_l;| +0 0] = e,_:,    (6.96)

^r2;l = (I — P2;l) ^_ ^ ( ¹ ~ 4.1)~ Wl^el:l +^rl;o] =

= 1 (l-e?.,)-ł[0 e,_;|+0) = 0    (6.97)

Widać, że dla 7 = 1 wszystkie sekcje, począwszy od n = 2 działają z zerowymi wartościami początkowymi, a więc:

♦ sekcjen = 2,. .._tN:

Pn, I = 0

Cn; I = C|;|

Tn.l = 0

Stąd wniosek, że dla 7 = 1 efektywnie działa jedynie sekcja n = I. zaś na wyjście filtru jest przesyłana (bez dalszego przetwarzania) próbka

(e/V;| = C|;|).

► 7 = 2

- Inicjalizacja algorytmu:

¥ próbka obserwowana: yi

*    estymacja wariancji Ci = AC| +yj ² cą = C₂

y\

*    próbka unormowana: y2 = ”

*    inicjalizacje sygnałów: e_0;2 = ^fo.2 = Tl

Cyfrowa filtracja aoaptacyjna szeregów czasowych

(6.91)

(6.98)

150

151

1

Zauważmy, że dla 7 = 0 wszystkie sekcje filtru działają z zerowymi wartościami początkowymi (współczynniki Schura i błędy w tył), toteż mamy:

♦ sekcje n = 1,..., N:

Pn.o = 0 e,.# = eo# = yo r„.o = 0

Stąd widać, że dla chwili 7=0 próbka yo jest przesyłana na wyjście filtru bez przetworzenia (e/v# = yo)-

2

7=1

- Inicjalizacja algorytmu:

♦    próbka obserwowana: yi

♦    estymacja wariancji: Cj = ACo + yf ; oj = c\

♦    próbka unormowana: yi = —

Komentarz: 0 < A < 1 jest tzw. „współczynnikiem zapominania” (35J, zmniejszającym wpływ odległej przeszłości sygnału Przyjęcie wartości A < 1 powoduje nałożenie na obserwowany szereg czasowy wagi typu eksponencjalnego. wskutek czego większy wpływ na estymatory paranie t rów filtru ma przeszłość „bliska " niż przeszłość „odległa " Innymi słowy, w takim przypadku mamy do czynienia z estymatorami krótkoterminowymi typu eksponencjalnego. Przyjęcie wartości A = 1 implikuje zastosowanie estymatorów długoterminowych. W celu szybszej estymacji Cr

XCj-1 +yj. dla początkowych wartości T = 1,2____można zatem przyjąć

A = I, a następnie uwzględnić wybraną (zależnie od konkretnego zastosowania) wartość tej stałej.

♦    inicjalizacje sygnałów: eo-.i = ro_;i = y\

- Algorytm:

+ sekcja n = 1 ((6.79)-(6.81) dla 7 = 1 oraz n = 0):

Pl;l = Pl:0( I    “ ^r0.o)^ “ ^e0.l ^r0;0 =

= 0 (1 — ej.l ) ^ ( I — ^r0.o) ^ ^e0.l ^r0;0 =

= eojro#    ⁽⁶ 92)