78273 P3200282

144

Z definicji iloczynu skalarnego mamy .V o .Vj = j.Y • ,V_: - cos j. gdzie

|iVj| = VI + 16 + 64 = y/Sl = 9

|JV| = _v/(A₁+A₂)’ + (5A₁)^j + (A,-A₂)’ =

= y/X\ + 2A₂A₂ + A* + 25Af + Aj -2A_tA₂ + X\ = v^7Af+2Af.

Skoro dla kąta j oraz dla kąta |x zachodzi | cos j| = | cos to należy rozpatrywać |jV@A'i[. Uwzględniając wcześniejsze obliczenia, dostajemy poniższą równość.

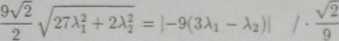
yj27X\ + 2X\ = |-V^/2(.3A₁ - A₂)|    /()²

27Aj + 2A^ = 2 ■ (9Af - 6A,A₂ + A$) 27Aj + 2Xl - 18Aj + 12A,A₂ - 2A§ = 0 9Aj + 12A₂A₂ = 0 3Aj • (3Ai + 4A₂) = 0 Aj = 0 V Aj = — -A₂

np. A₂ = -3 => Ai = 4

Jeżeli Ai = 0 i przyjmiemy A₂ = 1, wówczas otrzymamy płaszczyznę o równaniu £ — 2 + 4 = 0.

Natomiast dla A_t = 4 i A₂ = -3 mamy x + 20y + 7z - 12 = 0.

Odp.: Zadane warunki spełniają dwie płaszczyzny x - z + 4 = 0 oraz x + 20y + 7z — 12 = 0.

G7. Obliczyć odległość między prostymi /1, /₂, gdzie

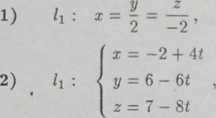
x - 9 y + 2

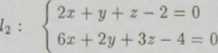
x — 7 y — 2 z

^{2 :}    -6    9    12

3)

i! 4    -3

1    _z_ _ y + 7 _ z — 2

^{2    :} -2 “    9    ” 2

W pierwszej kolejności zbadamy wzajemne położenie prostych /1, /₂, a następnie obliczymy odległość między nimi.

Ad G7.1)

I, • x = - = — . Ą(0.0,0), a, = [1,2.-2]

‘    2    -2

.    f 2* + y + *“² =°

** ^: \ 6» + 2* + 3r - 4 = 0

Wyznaczymy dowolny punkt leżący na prostej I₂ i wektor kierunkowy o,. Dla * = 0 mamy

( _y+ 2 = 2 => y = 2 - x \ 2y + 3x = 4 4 - 2x + 3x = 4

x - 0; y = 2

Stąd otrzymujemy punkt Ą(0,2,0).

! Gdyby przyjąć y = 0, to

f 2i + z = 2    .. f 2®+ z = 2

\ 6x + 3r = 4 /: 3    *    \2* + z= J

I Układ równań jest sprzeczny, zatem nie może być y = 0.

Prosta h leży w obu płaszczyznach, których jest krawędzią przecięcia, więc d₂ JL .V, = [2,1, l] i d₂ 1 N₂ = [6,2,3], stąd d₂ || fi_x X iV₂.

1 • i - 0 • J- 2 • fc = [1,0,~2]

Ni x Ń₂

1    j k

2    1 1 6 2 3

Możemy przyjąć a₂ = [1,0,—2]. Zachodzi

dj a₂ => Ii /A I₂ (proste nie są równoległe).

Proste Ii, Ij (nierównoległe) będą się przecinały, gdy wektory aj, a₂, P\Pi będą kompłaname, czyli gdy (di x o₂) o P, P₂ = 0. W przeciwnym przypadku proste będą prostymi skośnymi.

PTK 1 [0,2.0]

(d, X a₂) oP,P₂ =

1	2	-2		1 -2 1 -2
1	0	-2	= (-1)^3+2 -2-
0	2	0

= 0

Proste Ii, I₂ przecinają się, więc odległość między prostymi wynosi zero.