image 111

Obliczanie impedancji wejściowej anteny - metoda momentów 111

pojęcie iloczynu skalarnego funkcji w i g w postaci całkowej:

Obliczanie impedancji wejściowej anteny - metoda momentów 111

<w,g> =

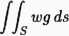
(6.41)

gdzie S jest brzegiem (np. powierzchnią) analizowanej struktury.

Aby uzyskać z (6.39) układ N niezależnych równań, pozwalający określić nieznane współczynniki a*, i = 1 ...N, „testujemy” wyżej omawiane równania, tzn. mnożymy je kolejno przez funkcje wybrane z szeregu funkcyjnego, tak zwanych „funkcji testujących” [ti/j], j = 1... N i obliczamy odpowiednie iloczyny skalarne. W efekcie uzyskujemy układ N równań:

N

Y,Oi<Wj₁L(g_i)> = <w_j,h>    (6.42)

i=l

gdzie j = 1...N

Równania (6.42) można zapisać w formie macierzowej:

(6.43)

[£)[«] = [h]

Rozwiązanie (6.43) znajdujemy za pomocą rachunku macierzowego:

(6.44)

Uważny Czytelnik zauważy, że przedstawiona procedura jest analogiczna do obliczania współczynników rozwinięcia funkcji okresowej w szereg Fouriera (przy założeniu, że funkcje bazowe i testujące są funkcjami harmonicznymi). W ogólności funkcje testujące powinny być liniowo niezależne, aby układ równań (6.43) był liniowo niezależny. Często jako funkcje testujące wybiera się funkcje bazowe. Ta odmiana metody momentów znana jest jako metoda Galerkina.

Warto zauważyć, że omawiano poprzednio metoda dopasowania punktowego jest w istocie metodą momentów, w której jako funkcje testujące wybrano dystrybucję deltę Diraca Wj — 5(r — f_m). Rzeczywiście, wykorzystując własności pseudofunkcji 6:

< L{9i),t(r-r_m) > = L(_gi) \? ₌    (6.45)

< h, Ó(r - f_m) > -    (6.46)

z (6.42) otrzymujemy (6.40).

Omawiając metodę momentów stwierdziliśmy, że wybór funkcji bazowych stanowi istotny etap tej metody. Dalej omówimy dokładniej to zagadnienie. Jak już wspomnieliśmy na wstępie funkcje bazowe powinny jak najlepiej przybliżać nieznane rozwiązanie, jakkolwiek teoretycznie możemy wybrać dowolny ciąg tworzący układ zupełny (np. szereg trygonometryczny). Należy jednak pamiętać, że jeśli funkcje bazowe dobrze przybliżają poszukiwaną funkcję,