DSC03968

-

198

ANTENY PROSTOLINIOWE

Rys. 9.5. Impedancja wejściowa dipola liniowego o promieniu 0.0005A. w funkcji długości L.

Linia kropkowana przedstawia rezystancję wejściową obliczoną ze wzoru dla dipola idealnego, linia przerywana dla dipola krótkiego.

zdefiniowanej dla zacisków wejściowych (R_pri). Moc promieniowana przez antenę wynosi

Ppr = yftRp™ jg    (9.18)

Dla dipoli będących nieparzystą wielokrotnością A./2 I_m = I_we i R_prm = R^. Trzecia definicja rezystancji promieniowania (Rp,) odnosi się do rzeczywistego maksimum prądu występującego w antenie. Dla dipoli krótszych od połowy długości fali maksimum prądu zawsze występuje na środku (zaciskach) dipola i Rpri = Rpf- W praktyce interesuje nas rezystancja wejściowa anteny, więc ważna staje się również R^. Prąd na zaciskach wejściowych dla dipoli zasilanych w środku jest równy

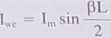
Wstawienie go do (10.1) daje

(9.19)

sin²(pL/2)

(9.20)

Tg

r — ^m r?

t2 ^xvprm ^Awc

R_prijest składnikiem rezystancji wejściowej anteny i jest równe przy pominięciu strat cieplnych (co zwykle będziemy czynić).

Dla dipoli o długościach L = X,2X,3X..., mamy pL/2 = 7i,27t,37t..., a ponadto rezystancja R_pri jest nieskończona. Będzie tak przy założeniu idealnie sinusoidalnego rozkładu prądu. Dipole o skończonej grubości mają bardzo duże, lecz skończone wartości impedancji wejściowej dla długości w pobliżu wielokrotności X. Oznacza to, że rozkład prądu dla tych długości nieco odbiega od założonego — prąd wejściowy ma zawsze skończoną wartość różną od 0.

Ponieważ przenikalność elektryczna przewodników jest nieco większa od 1, fala rozchodzi się wzdłuż anteny z nieco mniejszą prędkością niż w próżni. Na zmniejszenie prędkości ma ponadto wpływ pojemność rozproszenia anteny. Oznacza to, że długość fizyczna dipola nie jest równa długości elektrycznej. Redukując lekko długość dipola półfalowego otrzymujemy pracę anteny w rezonansie (X_wc = 0). Jego impedancja wejściowa wynosi wtedy ok. 70+j0 Q. Stopień skrócenia musi być tym większy, im większa jest średnica dipola, czyli przy małych współczynnikach smukłości. Najbardziej precyzyjnie można określić stopień skrócenia za pomocą metod numerycznych. Jeśli nie mamy do dyspozycji odpowiedniego oprogramowania, długość dipola półfalowego w rezonansie możemy obliczyć z zależności

rzecz

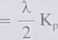
(9.21)

L,

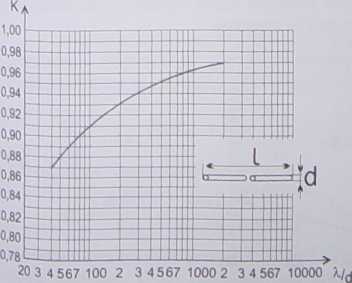
fys* 9.6. Współczynnik skrócenia dla dipola liniowego [3]