83624 skanuj0427

skąd

2 d sind = nX

Łatwo stwierdzić, że w przypadku odbicia Bragga spełnione są warunki rozpraszania przez wszystkie węzły sieciowe w zgodnej fazie (rys. 4.31 i 4.32), co, jak wykazaliśmy przy rozważaniu równań Lauego, jest warunkiem rozchodzenia się wiązki ugiętej:

1)    różnica faz między węzłami tej samej płaszczyzny jest równa zeru;

2)    różnica faz między węzłami należącymi do dwóch sąsiednich płaszczyzn wynosi nX.

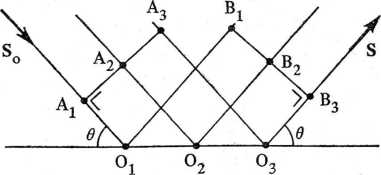
Rys. 4.31. W przypadku odbicia Bragga składowe pochodzące od węzłów tej samej płaszczyzny odbijającej nie wykazują żadnej różnicy faz. Istotnie

AiO_L-h 0₁B₁ = A2O2 + O2B2 = A3O3 + O3B3

Staje się to bezpośrednio widoczne po obróceniu wiązki odbitej o 180° wokół 0₁0₃, wskutek czego znajdzie się ona na przedłużeniu wiązki padającej

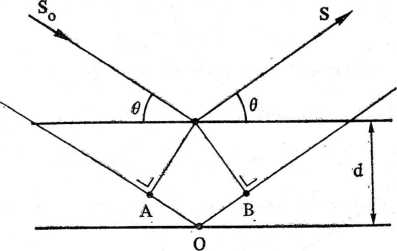
Rys. 4.32. Odbicie Bragga w-tego rzędu; AO+OB = wA, lecz AO = OB = dsind; stąd 2dsm0 = nX

Tłumaczy to, dlaczego dyfrakcja w kierunku S jest często nazywana odbiciem Bragga, a nawet, po prostu, odbiciem i dlaczego wiązki ugięte przez kryształ nazywa się wiązkami odbitymi.

Porównajmy równania Lauego

a • H = h' b • H = fc' c H = /'

z równaniem Bragga

2 d sinS = nX

Należy zauważyć, że dyfrakcja w kierunku

429