85960 img200 (2)

7. Sygnał wąskopasmowy.doc, 17/20

SYGNAŁ ANALITYCZNY (cd)

można również wyrazić sygnał x(t) poprzez sygnał x(t) z wyrażenia

X(co)= -ysgn(o))X(co)

wynika

X(co) = j sgn(co) X (co)

zatem

x(t)=-/(<)*    x{t) = -x(t)*/(/)= -x(/)* — = - \—<h

7t t n ^Ji:-t

wyrażenia

/ ^    1 °°r^x(^T) j

v)=- l

n ^Jt-t

—co

stanowią proste i odwrotne przekształcenie Hilberta

7. Sygnał wąskopasmowy.doc, 18/20

SYGNAŁ ANALITYCZNY (cd)

inny zapis

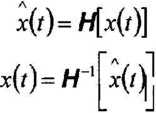
sygnał analityczny

z(/) = x{/)+ j x(t) = *(/)+ jhi[x{t)]

sygnał x(t) można traktować jako odpowiedź na sygnał x(t) filtru o odpowiedzi

h(t)- — oraz transmitancji //(co) = -jsgn(co) nt

x(t)	filtr	x(t) „
	kwadraturowy

filtr kwadraturowy realizuje przesunięcie wszystkich składowych o kąt - 90° w zakresie pulsacji dodatnich i 90° w zakresie pulsacji ujemnych, bez zmiany ich amplitud (filtr ten nazywany jest również filtrem Hilberta)