img199 (4)

7. Sygnał wąskopasmowy.doc, 15/20

SYGNAŁ ANALITYCZNY (cd)

zatem równość określająca widmo sygnału analitycznego Z_x{co) będzie spełniona tylko

wtedy, gdy widmo sygnału X(co) i widmo sygnału z nim skojarzonego A'(co) będą związane zależnością

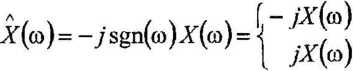
dla co > 0 dla co<0

7. Sygnał wąskopasmowy.doc, 16/20

SYGNAŁ ANALITYCZNY (cd)

Przekształcenie Hilberta

• ponieważ widmo sygnału skojarzonego x(/) jest iloczynem widm sygnału x(r) i funkcji - ;sgn(co), to sygnał ten jest splotem funkcji x(t) f(t), która jest odwrotną transformatą Fouriera funkcji - /sgn(eo)

ze względu na wygodę obliczeń przyjmijmy

- j sgn(co) = lim[- j sgn(co)]ćf

e—>0

wówczas

f(t) = — (I-;sgn(<o)]e^;"'Jo3 = limT-2- ]e^{c+J,)“'da--L    = —

’ 2iti^L K n-o 22nJ ‘j

czyli

kf)- /W*    40-    4>b/«- -7=¹ j*

nt n ii— t