238 (58)

METODY NUMERYCZNE.,

Aby określić współczynniki wybieramy w c- węzły 0}° i podajemy w nich parametry węzłowe — wartości funkcji v i jej pochodnych do odpowiedniego rzędu. Żądamy przy tym, aby warunki te określały jednoznacznie wielomian, w każdym e_: oraz aby funkcja v sklejona z tych wielomianów była ciągła w O. Przykłady konstrukcji przestrzeni podamy dalej.

Problem zbieżności MES, jak wiemy, sprowadza się do szacowania błędu interpolacyjnego (zob. twierdzenie 10.20). Dla rozważanej rodziny MES oszacowanie tego błędu podane jest w następującym twierdzeniu :

Twierdzenie 10.25 Jeśli

(1)    parametry węzłowe zawierają pochodne rzędu nie wyższego niż k,

(2)    lim inf a, '> a₀

*-o r

gdzie a_f- jest najmniejszym kątem trójkąta e_f, a_t, zaś jest stalą dodatnią niezależną od ft,

(3)    Pi(e_r) jest zbiorem wieloiwamów pełnych¹ A'-tego stopnia, i = 1,..., m_u. ro dla funkcji u e H^k'¹ r> JJ' prawdziwe jest oszacowanie

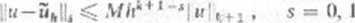
gdzie u_h ę V² jest funkcją interpolującą u, KI /aś jest stałą dodatnią niezależną od h.

Twierdzenie to podajemy bez dowodu. Dodajmy, że przy przyjętych założeniach idea tego dowodu jest taka sama jak dowodu twierdzenia 10.21. Powyższe twierdzenie a także poprzednie o oszacowaniu błędu interpolacyjnego są szczególnymi przypadkami ogólnego twierdzenia o błędzie interpolacji w przestrzeniach Sobolewa, które można znaleźć np. w pracy [14].

Przechodzimy do przykładów konstrukcji przestrzeni V^^k) dla k = 1,2,3. (a) Przestrzeń K^<1J. W tym przypadku r e Pj¹ⁿ(Q) ma na c_t postać

V\_e( (.V) = Cort + cio4^{1 c}oi ^x2

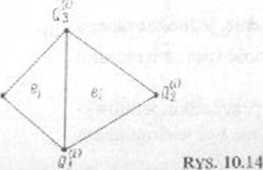
Za węzły przyjmujemy wierzchołki trójkąta e_:, które oznaczamy Q¹}\j -1,2. 3. zob. rys. 10.14, natomiast za parametry węzłowe przyjmujemy wartości v w tych punktach, tj (Qj^,})-

1

Rozumiemy prz.cz io. że wielomian ma niczerowe współczynniki przy jednomianach

2

x'x^r gdzie s, r są dowolnymi nieujemnymi liczbami całkowitymi takimi, że s+r k.