Image0008 (3)

J.Stadnicki Optymalizacja- wykład dla Mechaniki, część4: PROGRAMOWANIE NIELINIOWE — metody numeryczne 15

J.Stadnicki Optymalizacja- wykład dla Mechaniki, część4: PROGRAMOWANIE NIELINIOWE — metody numeryczne 15

Algorytm Powella:

1° dla fc = 0 przyjmij t^k =0 oraz krok t,

2° oblicz t^k 1 =t^k -\-t oraz Q {t^k ) i Q (t^k41),

3° jeżeli Q{t^k ' )>Q{t^k) dla A; = 0 to odwróć kierunek poszukiwań,

4° jeżeli Q {t^k *¹ )<Q{t^k) to podstaw t — 2t i powtórz krok 2°dlaA; = k-\-l,

jeżeli Q{t^{L l})>Q{t^K) i k>l to podstaw

i — 0,5t i oblicz Q {t^k^^] —t).

Otrzymamy trzy punkty A.B,C w równych odległościach t od siebie.

ze wzoru

5° przez punkty A, B, C poprowadź parabolę interpolującą i wyznacz jej minimum (4.13).

6° jeżeli

Q(t*)

— --<e, to przyjmij x = x_] -\-t ,

w przeciwnym przypadku powtórz obliczenia z punktu B z krokiem o połowę

J.Stadnicki Optymalizacja- wykład dla Mechaniki, część4: PROGRAMOWANIE NIELINIOWE - metody numeryczne    16

ALGORYTMY GRADIENTOWE

Wykorzystują znajomość pierwszej pochodnej funkcji Q [X), która musi być różniczkowalna i jej pochodną powinno dać się wyznaczyć w sposób jawny.

Wykorzystują dwie strategie:

a)    szukanie miejsca zerowego pochodnej,

b)    interpolowanie funkcji wielomianami wyższego stopnia, np. interpolacja sześcienna.

ALGORYTM SIECZNYCH

1° dla k = i) podstaw x^k —d,

xl=b,

2° oblicz Q' (x^k) i Q' (x^k2 ),

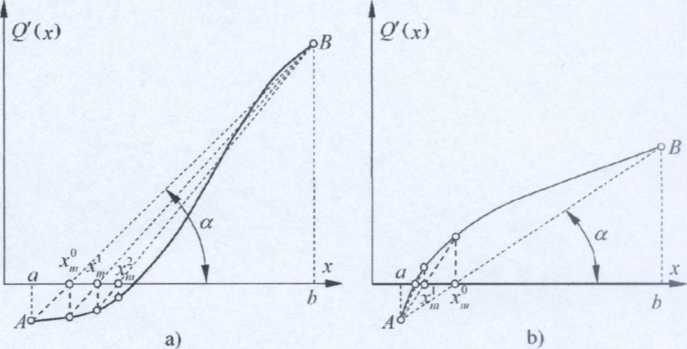
Niech Q{x) jest wypukła klasy

c^] i ma minimum wewnątrz przedziału

Algorytm: