Image0010 (3)

J.Stadnicki Optymalizacja- wykład dla Mechaniki, część4: PROGRAMOWANIE NIELINIOWE — metody numeryczne 19

ALGORYTM NEWTONA"

Q{ x)jest jednomodalna i klasy C¹.

W otoczeniu x^k przybliżymy Q {x)za pomocą szeregu Taylora z dokładnością do wyrazu z drugą pochodną (aproksymacja kwadratowa):

Q(x)^F_t (x)=Q{x^k)+Q'(x^t)(x-x^k)+-Q"(x^k){x-x^kf    (4.17)

2

Równanie (4.17) przedstawia parabolę F_k{x) , którą potraktujemy jako przybliżenie funkcji Q(x). Ma ona minimum w wierzchołku , którym przyjmiemy za przybliżenie punktu X będącego minimum funkcji Q (x).

F'«)=Q'(x*)+«''(x‘)(x:-x‘)=0    =>    < = x‘-^]    <*•«• ³ Algorytm znany jest również w literaturze jako algorytm Newtona-Ra phsona

J.Stadnicki Optymalizacja- wykład dla Mechaniki, część4: PROGRAMOWANIE NIELINIOWE - metody numeryczne    20

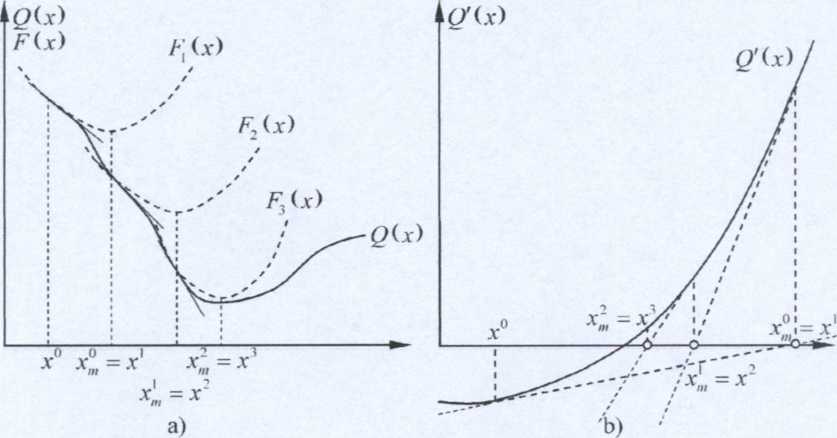
Algorytm osiąga największą zbieżność dla Q¹¹ {x^k)—>0 (zbieżność kwadratowa).

Przenosząc zadanie z płaszczyzny    x)} na płaszczyznę {x, Q'( x)}, zamiast szukać mi

nimum Q{x), możemy poszukiwać miejsca zerowego pochodnej Q^f (x) za pomocą stycznych do jej wykresu (rys. b).