286 (8)

O eon a dokładności

1) Błąd położenia punktu

- macierz kowariancji wyrównanych współrzędnych

Ć* =/i^(A⁷PA)“'

f 50.58	- 37.94"	r -> _|	ćov(Xz.Yz)
j -37.94 i.	50.59	(mm) | cm’(f	O Yy. J

- błędy średnie wyrównanych współrzędnych i błąd położenia punktu Z

ni - — 750.58 —7.1 (mm) 1 A /
		i 1 2
»iy — J50.59 — 7.1 (min) I		^mptĄZ) ~yj^mx./ ^+/Uyy

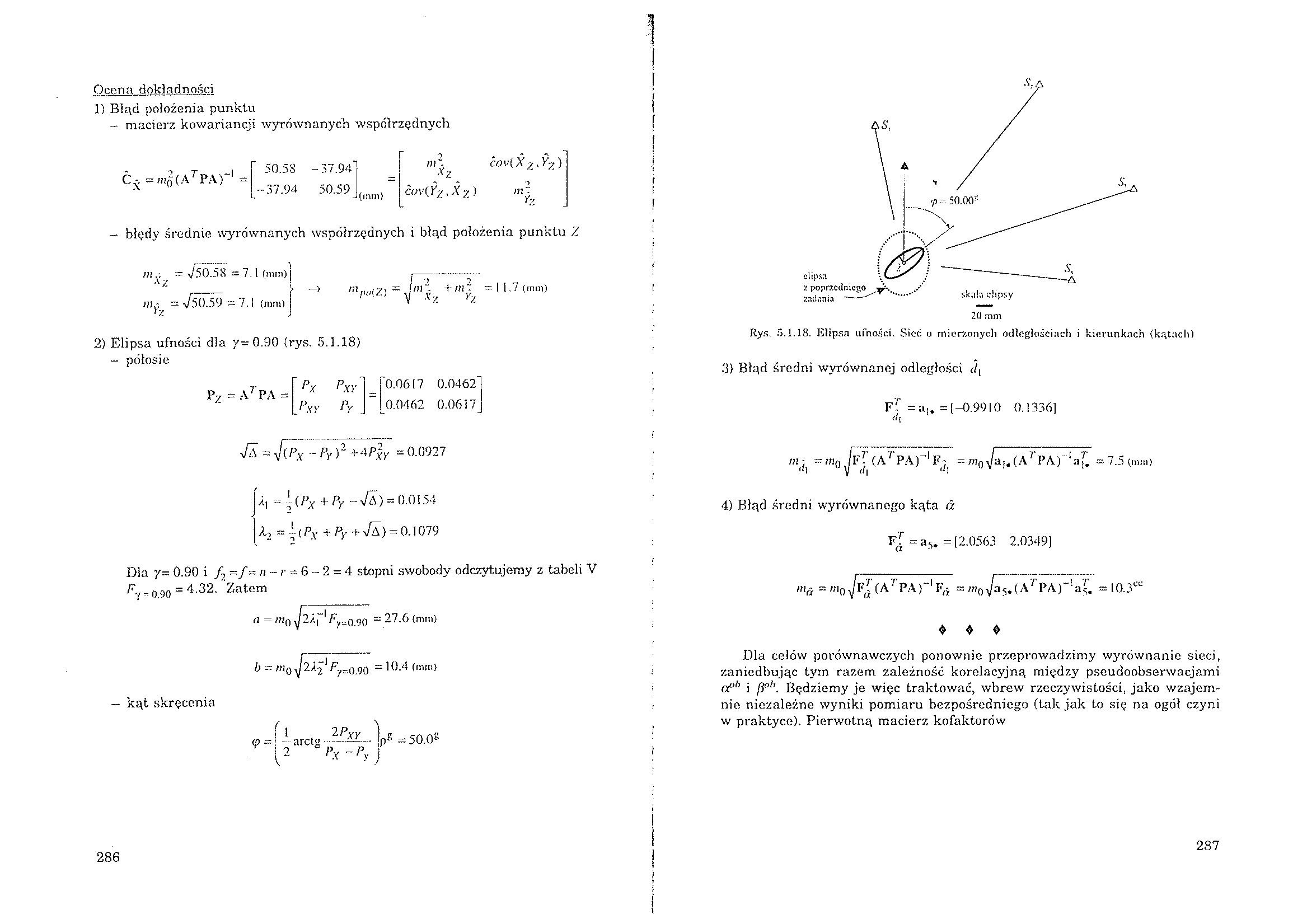
2) Elipsa ufności dla y=0.90 (rys. 5.1.18) - półosie

Px

P_X Y

0.04621

0.0617 J

P_z = A⁷ PA =

p_Yri r°.o6 [7

I\ ~ [ 0.0462

!’_x — Py)“ +4P_xy - 0.0927

2, =i(P_x +Py ~yfi\) ~ 0.0154 l₂ ~ ' ( P_x -t- Py + yfA ) = 0. 1 079

Dla y- 0.90 i Ą =/= ;j ~ r = 6 - 2 = 4 stopni swobody odczytujemy z tabeli V /fy _ _{0 90} = 4.32. Zatem

a = m_{) b = m₀

^y-0.90

— 27.6 (mm)

f'y-.0.9Q

-10.4 (mm)

— kąt skręcenia

X

- 50.0⁸

1    2P_Xy

.....aretg.....——■

2    ^hP_x-P_y

z poprzedniego w-.    ./    , ,    ..

,    ___*......‘    sk;i a c ipsy

Zndnnia    ¹ ’

20 mm

Rys. 5.1.18. Elipsa ufności. Sieć u mierzonych odległościach i kierunkach (kątach)

3) Błąd średni wyrównanej odległości </,

F-f = a,. =(-0.9910 0.1336] <h

~ ^m0

4) Błąd średni wyrównanego kąta a

-.7

JfJ (A^tPAr‘ F_?J - m_Q \/aj7(A⁷ P A) ¹ a f. = 7.5 (min)

Fi = a₅. =12.0563 2.0349]

* = /ao^CA^PA)"¹^ = m₀^^(A^rPAy^l-.ii = 10.3"

Dla celów porównawczych ponownie przeprowadzimy wyrównanie sieci, zaniedbując tym razem zależność korelacyjną miedzy pseudoobserwacjami tt"⁷* i Będziemy je więc traktować, wbrew rzeczywistości, jako wzajemnie niezależne wyniki pomiaru bezpośredniego (tak jak to się na ogół czyni w praktyce). Pierwotną macierz kofaktorów

287