276 (10)

ii* i mm

,n.*-

sprowadzenie obu

- stron do równych

⁶ podstaw

Nierówności logarytmiczne

Założenia: *-5>0, czyli x > 5

I sposób na P⁰<j"    .    ' 5) = log₂

Siedefinicj-

^,V6J\    _ n

logaiytmu •'    1

(pifl03.lL):    13 «(*.+»)

'%_5 = 2³    Odp. * ⁼¹³

,_vi 13 e;(5;⁺⁰°)

©dp..v= 13

Odp.AT= 13

porównanie wyrażeń logarytmowanych po opuszczeniu loga-rytmów o wspólnych podstawach rozwiązujemy w wyznaczonej na początku dziedzinie wraz z odpowiedzią

D„_r⁼ (5; +00) log₂(* - 5) < log₂8

podstawa logarytmu a = 2 e (l; +00' kierunek nierówności zachowujemy *-5<8A xe.D_m x< 13 <rvxW

5    13

Odp. i e (5; 13)

log_I(x+!) + l°g_I(x+2) = 2

x>-l

Założenia: x> -2    ,

jc > 0 A a: # 1 D = (0;l)u(l;+oo)

*°8.(^x+ l)(* + 2) = 2 z definicji logarytrau *^!+3x + 2 = *^J

I

^x=-\iD_t

°dp- Brak rozwiązań.

wyznaczanie

dziedziny

skorzystanie z praw działań na logaiytmach

sprowadzenie obu stron nierówności iogaiytmów o jednakowych podstawach Podstawa a = z jest nieznana, więc "nieży rozwiązać nierówność w obu ^wersjach: ze zmianą Kierunku

. nierówności w 1°

nierówności w ₂. +

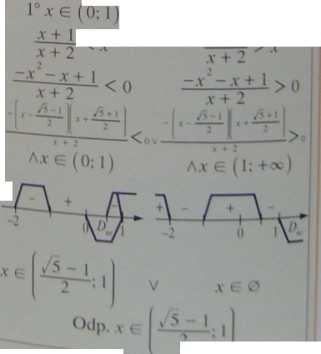
log_x(x+l)-lo_g;t(A: + 2)>l x>-\

Założenia: ■ x > -2    ,

x> 0Ax#1 Z)_nr=(0;¹)u(¹;+°o)

> 1

'* + 2

r^g-fTł^>Iog**

są dwa przypadki

2°x e (1; +00) ■    x+\