298 (9)

na podstawę wyrównanych współrzędnych

(ll ~	yl(X2}-X |3)^; + (>31	~7jł)” — 1674.85 (m) v
(I2 — \	/(*2l - A"20)“ +(>2I	_y20)^2 =1694.10 rm) v
<h =!	/(X21 ~ A 20)" (>2i	- “ = 1367,67 (nu v

_v \

H etap kontroli na podstawie poprawek.

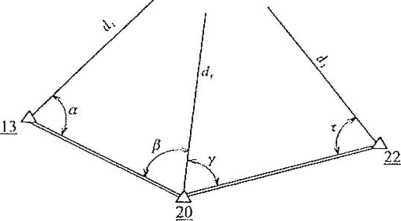
rf, = 1674.85 (in)

<i'i ~ i 694.10 (mi (i 2 ~ 1367.67 (m>

a ret a

(

r = i arctc

>20	- aretg	>21 -
*20- *13		* 21 ''
>21 ~ *20		>13-
*21 ~ *20		*13 —
>22- >20		>\l“
A 22 “ A 20	aretg	*21 —

731 — 7'7 4 2 j ~ A -

42ⁱ’57'33' v

o = 56^c34'05" v

a * 42*57'33"

fi ~ 5 6° 34'05"    P ~

y - 62° 51'33'

-?I........—°-)o = 62"5l'35"

X 'rn )

i - 45\55'29'

r = aretg •

}⁷20

■aretg—™ *20

“ >22 - Ar-

o = 45°S5'29'

Ocena dokładności

1) Błąd położenia punktu 21 po wyrównaniu

- macierz kowariancji wyrównanych współrzędnych

= /»q (A^rPA)

O

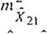
cm>(y_2l, X 2|}

0.00079 0.00020] 0.00020 0.0008 lj_(|nlz

^C0V(^X2l'^Y2l)

1

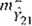
błędy średnie wyrównanych współrzędnych i błąd położenia punktu

s/o.00079 = 0.03 (m) |

>n

* 21

mc = /0.00081 - 0.03 (m) '21

">    'ⁿ}u>(2\)    ^+,r‘y₂i

~ 0.04 (m)

2) EHpsa ufności dla y~ 0.90 (rys. 5.1.20)

A⁷" PA =

^PX ^pXY ] _ f 2286.5116 -574.3190] _P_Xy Py J ~ [- 574.3190 2225.0756 J

- pófosie

JA = yj(P_x Jpy)¹ t4PŹ_y - 1150.2799

I Aj = - (Pv +Pv~J,A) = 1680.6535 1 ²

[    - i{p_x + P_Y-f Ta) = 2830.9335

dla 7- 0.90 i/₂ =/= /i-/-= 7- 2 = 5 odczytujemy F = 3.78

rt — tn₀ J2A| ^l/'._/_Q go — 0.09 <m) /; =    ¹ 7'y-o.90 ⁼ 0.07 (m)

- kąt skręcenia

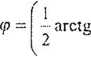
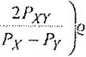
—f3'^ł47'

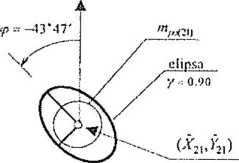
skala elipsy i m 0.10 m

Rys. 5.1.20. Elipsa ufności i błąd położenia punktu

299