303 (8)

^•"Odul

flU

Czyli być może dla r =

Stą,.

ynjiary 'kulę by jego 'ksza?

any

rwo)

o

zaś/i - = ?/

'271’

fW

71 ‘

jtS zadania poleca wyznaczyć ircitóbtl zmienną, aby zbudowana g^cja osiągała wartość optymalną ■antmalną). Stosujemy w tym celu 'jjwack pochodnych (por. 11.3.2b. ilU,2c.): rozwiązujemy warunek wiieczny i sprawdzamy warunek wystarczający.

^stwierdzeniu ekstremum obliczany pozostałą szukaną zmienną.

r > 0

Z warunku koniecznego na ekstremum:

P_c'(r) = 0«27tr^J-V=0»

nr

.271

jest P_r(r) najmniejsza, ale trzeba się o tym przekonać, sprawdzając warunek wystarczający na ekstremum:

i \ /

/!,= <) V/l,= ^fl (/i, = 0 nie należy do dziedziny, zaś h₂ = 41 należy do dziedziny).

Czyli być może dla h = ^ R jest V(h)największa, ale trzeba się o tym przekonać, sprawdzając warunek na ekstremum:

v. S \

V'\    +

WięC^-fR,

tfllisp

tak aby

Formułujemy odpowiedź.

Odp. Dla r = y-^ih i y-jj-pole powierzchni walca osiąga wartość najmniejszą.

Odp. Dla h = y R i 2 Jl

r - —j— R objętość stożka jest największa.

'pisania

ikąt:

Uwaga: W każdym z powyższych przykładów można ponadto obliczyć optymalną wartość funkcji celu:

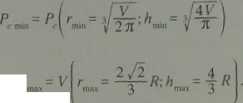
oraz V___= V

- j7tA^J innej - h (stopnia) ikowalńą

1. Jeśli funkcja celu jest funkcją kwadratową (por. 3.3.2.), wówczas można obliczyć ekstremum tej funkcji bez rachunku pochodnych, wykorzystując ekstremum funkcji kwadratowej.

zsumowując tok rozwiązywania w zadaniach optymalizacyjnych, stwierdzamy, iż istota postępowania Pkp na znalezieniu wzoru różniczkowalnej funkcji celu ustalającej zależność między poszukiwanymi ^nymi. Następnie wyznacza się ekstremum (lokalne) tej funkcji. Można tego dokonać na dwa sposoby:

II. Jeśli funkcja celu nie jest funkcją kwadratową (por. 11.4.1.), wówczas obli-lub czarny ekstremum tej funkcji, wykorzystując rachunek po-• chodnych dotyczący związku pochodnej z ekstremum funkcji.