332 (7)

lenia wzajemnego położenia punktów brakuje trzech obserwacji {np. odległości). Taką też wartość ma defekt wewnętrzny, czyli d_w = 3. Defekt całkowity sieci jest więc równy d = d. -f- d_w = 6 (rys. 5.2.7).

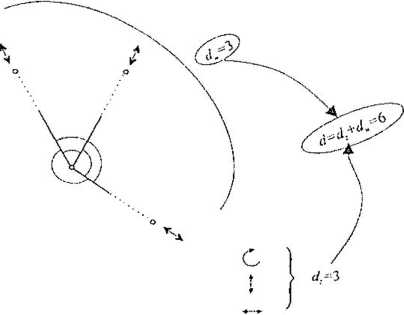
Rys. 5.2.7

> y

W sieci występują cztery punkty o nieznanych współrzędnych (X, Y). Zatem r - 4-2    8. Skoro d ~ 6, więc rzeczywiście

f = /i - r -l- d -■ 4 - 8 + 6 = 2

co oznacza, że należy utworzyć dwa wzajemnie niezależne równania warunkowe. Po utworzeniu tych równań oraz dalszych działaniach, podobnych jak w poprzednich przykładach, uzyskujemy (można zastosować także inny zestaw równań):

a, +a₂ +% -400^g = 0 OTj -va2 -or₄ - 0

v, + v,    +

V| +V₂    - V₄ +

af+af +af -4006 ^0 ^A\

af + af -af ~ 0 skąd

1 l 1 o'	A —	A |		50
_l l 0 ~1_	i\ —	Ai.		20_

Na podstawie wartości błędów średnich pomiaru kątów, wyznaczamy macierz wag, a w zasadzie interesującą nas w obliczeniach jej odwrotność P"¹

1 -) m~ ^a2		400 400
^a7 ->		400 100
L j

Następnie, obliczając

-0.00182'

0.00273_

-11.8'

-11.8 -26.4 -3.6    ,

J(Cc)

I etap kontroli

j = V⁷>V =2.568]

> $ — s'

s' ~-k^? A = 2.568j

uzyskujemy wyrównane kąty o wartościach:

di =af + vj - 42^g12^c40^cc - 12^cc ~ 42^K12^C28^CC a o - af + v₂ ~ 121^g24^c45^cc - 12^cc = I2l^g24^c33^cc d₃ - af + v₃ = 23ó^g63^c65^cc - 26^cc = 236^g63^c39^cc

a_Ą = af + v₄ = 163^g36^c65^cc - 4^cc = 163^g36^c61^cc

II etap kontroli, to sprawdzenie, czy wyrównane kąty spełniają równania warunkowe

di -ł-ór₂ + «3 -400“ = 0 dj +a₂ -d₄ = 0

BP^_IB⁷ =

1200 800 800 900

(BP“^IB⁷)’

0.066

0.036

0.00204

■0.00182

V =P^_,B^rk

42^g12^c28^cc + 12I⁸24^c33^cc + 236^g63^c39^cc ~400^g = 0 42^g12°28^cc + 121^g24^c33^cc ~163^s36^c61^cc -0

v

333

v