406 (4)

tów. W ten sposób jest definiowany lokalny układ współrzędnych, natomiast współrzędne go definiujące są w takich rozwiązaniach wielkościami stałymi i nie podlegają wyrównaniu (przemieszczeniu). Oznacza to, że niektóre z punktów sieci dotąd swobodnej, odgrywając rolę punktów stałych (lub częściowo stałych), są traktowane w sposób szczególny, przy czym wybór takich punktów jest, w zasadzie, dowolny. Rodzi to problem niejednoznacznej oceny dokładności położenia punktów. Zauważmy bowiem, że błąd położenia punktu wybranego jako stały jest równy zeru. Podobnie, odpowiadająca mu elipsa ufności jest zredukowana do punktu lub odcinka, gdy założono stałość tylko jednej ze współrzędnych. Tę samą sieć można jednak wyrównać ponownie, przyjmując inny punkt jako stały. Wówczas ten poprzedni otrzyma jakąś elipsę ufności, natomiast aktualnie wybrany - tym razem jest „bezbłędny”. W takiej sytuacji trudno więc formułować obiektywne wnioski o dokładności położenia punktów sieci, rys. 9.2 (są metody oceny obiektywnej, lecz dotyczą one elips ufności pewnych funkcji, niezmienniczych względem układu współrzędnych, np. Gażdzickj 1976).

Wyrównanie swobodne można zastosować nie tylko do wyrównania swobodnych sieci geodezyjnych. Traktując ten sposób optymalizacji w szerszym sensie, można także, o czym będzie mowa w rozdz. 10, poszukiwać odstających punktów dostosowania.

Współrzędne punktów stałych (punktów dostosowania) w dowiązanych sieciach geodezyjnych są wyznaczane na podstawie jakichś wcześniejszych

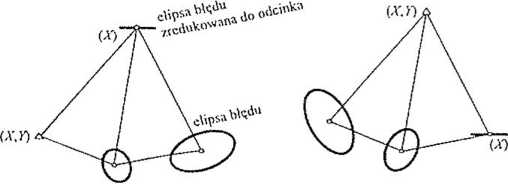
Y) - punkt o stałych współrzędnych X,Y (A") - punkt o stałej współrzędnej X (Y) -- punkt o stałej współrzędnej Y

Rys. 9.2. Ilustracja niejednoznacznej oceny dokładności położenia punktów w sieciach

swohodnych

pomiarów, a więc także są obarczone pewnymi błędami. Na ogół dokładność współrzędnych takich punktów nie ma istotnego wpływu na dokładność wyznaczenia nowych punktów. W rzeczywistości, niektóre z punktów stałych mogą jednak wykraczać poza deklarowane przez odpowiednie parametry do-kładnościowe obszary dla nich dopuszczalne. Takie punkty będziemy nazywali odstającymi punktami dostosowania. Ilustrując ten problem, przyjmijmy, że w przykładzie 5.1.5 inżynierskim zadaniem jest wyznaczenie współrzędnych punktu 21, powiedzmy z taką dokładnością, aby błąd położenia tego punktu był mniejszy od 10 cm (m^_rJ<0.10 m). Ufając, że błędy położenia punktów stałych Q3, 20, 22) są odpowiednio mniejsze (np. n\,_m < 0.02 m), wykonano pomiary kątów i boków z dokładnością wystarczającą do osiągnięcia przyjętego celu. Niech w rzeczywistości, na skutek różnych powodów (np. nierzetelności w analizie dokładności sieci, do której należą punkty stale, naruszenia stabilizacji tych punktów, itp.), któryś z nich leży daleko poza odpowiednim dla niego obszarem ufności. Nie mając o tym wiedzy i prowadząc w „dobrej wierze” proces wyrównania, a więc dostosowując wyniki pomiaru do warunków narzuconych m.in. przez punkty stałe, w istocie możemy pogorszyć rezultaty bezpośrednich pomiarów. Na rezultaty wyrównania będą bowiem miały wpływ nie tylko błędy aktualnego pomiaru, lecz także niedopuszczalne, błędne położenie odstających punktów dostosowania. Na podstawie uzyskanych wartości (szczególnie dotyczących analizy dokładności) oraz wobec braku wiedzy o rzeczywistej ich genezie, niesłusznie będziemy sądzili, że to właśnie wyniki pomiaru nie spełniają wymaganych kryteriów dokładnościowych, czy też, że w ich zbiorze istnieją obserwacje odstające. Takie błędne rozpoznanie może mieć konsekwencje ekonomiczno-techniczne, polegające na podjęciu decyzji o ponownym pomiarze z użyciem sprzętu o wyższej dokładności, co bez odrzucenia odstających punktów dostosowania w dalszym ciągu nie rozwiąże zaistniałego problemu.

9.2. Teoria wyrównania swobodnego*

Wcześniej wskazaliśmy, że możliwym do przyjęcia estymatorem przyrostów w swobodnej sieci geodezyjnej jest estymator

d x ~~ ^ !>p^ ^

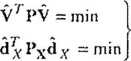
(9.2)

spełniający kryteria (9.3) *' Na postawie m.in.: Mittekmayer (1972). Pbu.kr (1980), PEitEi.MUTER (1979, 1980), Prószyński (1981), Woi.F (1972, 1979).

407