442 (5)

I ODPORNE WYRÓWNANIE SWOBODNE

10.1. Założenia podstawowe

Wpisowa dzenie

We wprowadzeniu do poprzedniego rozdziału wspomnieliśmy, że w praktyce mogp wystąpić sytuacje, gdy współrzędne punktów dostosowania, z różnych powodów, są obarczone dużymi błędami. „Uwalniając" sieć geodezyjną od stałości tych punktów oraz stosując wyrównanie swobodne, można się spodziewać, że wyznaczone tą drogą przyrosty do współrzędnych punktów odstających (podobnie jak poprawki clo odstających obserwacji, zob. rozdz. 8), będą stosunkowo duże (rys. 10.1).

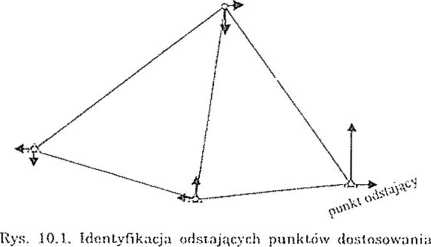
W tym rozdziale przedstawimy taką wersję odpornego wyrównania swobodnego, w której przez odpowiednią modyfikację (tłumienie) elementów macierzy wag P_x następuje zmniejszanie wpływu odstających współrzędnych punktów dostosowania na ostateczne wyznaczenia (punkty odstające można także identyfikować w trakcie wyrównania sekwencyjnego, stosując, odporną estymację bayesowską, Kamiński 2000).

Ogólna idea odpornego wyrównania swobodnego jest podobna do tej, która jest podstawą omawianego w rozdz. 8, wyrównania wyników pomiaru odpornego na błędy grube (z zastosowaniem funkcji tłumienia). Tam identyfikacji oraz zmniejszaniu wpływu podlegają obserwacje odstające, tutaj -odstające przyrosty do współrzędnych punktów, w omawianej wersji — do współrzędnych punktów dostosowania. W jednym i drugim przypadku „wyciszanie” wpływu może być realizowane przez tłumienie macierzy wag: tam macierzy wag P wyników pomiaru, tutaj - macierzy wag P_x (w pracy Czapiewski 2004 przedstawiono metodę łączącą te zagadnienia).

Punkty dostosowania w klasycznych metodach wyrównania, o czym już wielokrotnie mówiliśmy, są traktowane jako stale, tzn. jako punkty o bezbłędnych współrzędnych. Takie założenie jest pewnym uproszczeniem, gdyż w rzeczywistości współrzędne tych punktów są także zmiennymi losowymi o ustalonych wartościach błędów średnich. W dobrych procedurach inżynierskich zakłada się jednak, że spodziewana dokładność położenia nowych punktów jest dużo mniejsza niż* dokładność położenia punktów dostosowania. Jak wiemy, w praktyce problem ten rozwiązują klasy dokładności sieci geodezyjnych i nienaruszalna zasada, że sieci powinny być do wiązywane tylko do punktów o wyższej niż one same klasie dokładności. Wówczas wpływ losowego położenia punktów dostosowania (w dopuszczalnym obszarze) może być zaniedbywany. Dopiero wtedy można także mówić o ich relatywnej bezbłędności (stałości). Warto przy tej okazji wspomnieć, że wpływ błędności punktów dostosowania można uwzględnić w wyrównaniu klasycznym, odpowiednio formułując macierz kowariancji wyrazów wolnych, tzn. wprowadzając do funkcji L = F(X-j)-n, oprócz wektora współrzędnych przybliżonych. punktów wyznaczanych, także wektor X^- współrzędnych punktów dostosowania o macierzy kowariancji C_x . Wówczas

C_r.

—------------ L\'    ------------------! 'r U-

3X.v ^Xi[ 3X._V j

Przyjmijmy, że elementy wektora X^ są na tyle słabo od siebie zależne, że do celów określonych w t.ym rozdziale, kowariancje między nimi można uznać za nieistotne. Zakładamy więc, że współrzędne (X.s' .*5 > punktów dostosowania S-, j 1.....n_s, są zmiennymi losowymi wzajemnie niezależny

mi, a także niezależnymi od wszystkich inny cli elementów wektora X^ (niekiedy takie założenie będzie trudne do zaakceptowania, jednak wobec braku informacji o wszystkich elementach macierzy C_X(j. — jedyne możliwe do przyjęcia). Niech współrzędne punktów dostosowania będą wyznaczone z błędami średnimi ..., w_y . Dla wygody dalszych działań, głównie tych o charakterze numerycznym, przyjmiemy, że również współrzędne przybliżone (Xy <Yy ) punktów wyznaczanych Z., /~ 1,.są określone z błędami

średnimi m o    Hub przynajmniej, że współrzędnym tym są przypo-

Zi Zi

rządkowane odpowiednie wagi). Powyższe założenia umożliwiają przyporządkowanie wszystkim współrzędnym sieci geodezyjnej następującej diagonalnej macierzy wag P_x:

443