446 (9)

przypada dla dyskretnych wartości częstotliwości i widmo takie nazywane jest widmem prążkowym. Pierwsze trzy przykłady z ryc. 15.5 przedstawiają widma tego typu. Sygnał sinusoidalny z definicji zaw iera tylko jedną składową. Fala prostokątna składa się z nieparzystych harmonicznych składowej podstawx>wej. których amplitudy maleją ze wzrostem numeru harmonicznej. Ciąg impulsów powtarzających się o stały przedział czasu zawiera wszystkie składowe harmoniczne składowej podstawowej o równych amplitudach.

W praktyce szereg Fouriera nie mo/c być stasowany do analizy częstotliwościowej sygnałów, ponieważ w rozważaniach teoretycznych zakłada się nieskończony czas trwania przebiegu, podczas gdy zjawiska obscrwsiwanc w praktyce mają skończony czas trwania. Ponadto zakłada się okresowość przebiegu /(f). a tymczasem przebiegi występujące w rzeczywistości są często meokresowe. Aby ominąć te trudności, dla zdeterminowanych przebiegów nieokrcsowych oraz dla sygnałów niezdeterminowanych zakłada się. że jedna realizacja o okresie T jest całym przebiegiem. Funkcję/t#) można przedstawić w postaci:

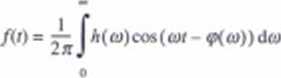
(15.13)

Wyrażenie (15.13) nazywamy przekształceniem (transformacją) Fouriera i ozna cza ono. że przebieg /(/) można zapisać za pomocą jego widma amplitudowego h{a>) i fazowego (p(c/). Przekształcenie Fouriera można uważać za odpowiednik szeregu Fouriera dla sygnałów nieokrcsowych. Pozwala ono tu przedstawienie funkcji nieperiodycznej jako sumy nieskończonej liczby składowych periodycznych. O ile jednak szereg Fouriera dawał tak zwane widmo prążkowe, o tyle w wyniku zastosowania całki Fouriera otrzymuje się widmo ciągłe. W ogólnym przypadku dźwięki nieperiodyczne mają widma ciągle. W widmach ciągłych niezerowc amplitudy składowych nic przypadają na dyskretne wartości częstotliwości, ałe na określone jej pasma. Ostatnie trzy przykłady z ryc. 15.5 ilustrują w idma ciągłe. Pojedynczy impuls, podobnie jak szum biały, ma płaskie widmo amplitudowe, tzn. amplituda nic zmienia się ze zmianą częstotliwości. Pomimo że impuls i szum mają w idma tego samego kształtu, amplitudy poszczególnych składowych widma impulsu są mniejsze od składowych szumu, ponieważ impuls niesie znacznie mniej energii niż szum. Impuls i v/um różnią się widmami fazowymi (nic pokazanymi na ryc. 15.5). przedstawiającymi zależności fazy składowych od częstotliwości. Fazy składowych szumu mają rozkład przypadkowy, natomiast wszystkie składowe impulsu w chwili / s 0 mają fazę 90^. W rezultacie, w czasie / ■ 0 wszystkie składowe sumują się. podczas gdy dla innych wartości czasu składowe te znoszą się.

Ostatni przykład na ryc. 15.5 ilustruje kilka następujących po sobie okresów sinusoidy. nazywanych impulsem tonu. Dla długiego czasu trwania widmo sygnału sinusoidalnego jest pojedynczym prążkiem. Widmo impulsów tonu o krótkich czasach trwania zaw icra energię w paśmie częstotliwości otaczającym nominalną czę-

446