48 (169)

ł- Funkcje I ich włoieołtl

własności funkcji (por. 2.1.6.)

i górna

pólpta- ^: ********

_|01_

osiąOX)

(znak dodatni)

fl*>

(miejsca zerowe) (wykres pod osia rm 1

'1 szczycą*

A więc:

J~(^x) > O dla *: «EE ( — 5; — 1 ) U (i; 3.7\ - funkcja jest znaku dodatniego,

y(jc) < O dla jc €= f—1;-Ł\ U (3.7; 8) - funkcja

jest znaku ujemnego, f) Monotoniczność (por. 2.1-ód.)

Monotoniczność funkcji, której wykres jest przedstawiony na rysunku, można zilustrować następująco;

f “ /oonst    //    /\ f consi    / "

6    7    8 AT

—5

Ja punkt (3:3) (najwyżej |

_Hłhdi*tt> k a watio-wi

najmniejsze

2.5.2. Odczytywanie x iei wykresu

Największą rolę w analizie określonego fragmentu rzeczywistości odgrywają wykresy prezentujące własności i dynamikę wybranych zjawisk. Analizując wykres (model), można wyciągać różne wnioski o przebiegu przedstawianego zjawiska.

Oto podstawowe własności, które odczytujemy, analizując wykres określonej zależności funkcji (por. 2.1.5. i 2.1.6. oraz z 2.2.1., 2.2.3. i 2.2.4.).

Dany jest wykres funkcji y =/(.r):

(|xtoomc Mimiki omteajc proswkmny rcut wyłcresu na oś OV)

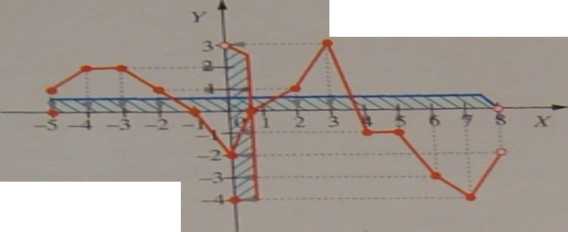
(pionowe strzałki oznaczają prostokątny rzut wykresu na oś OAT)

Na podstawie wykresu będą odczytywane niżej wymienione własności funkcji.

a)    Dziedzina i zbiór wartości (por. z 2.1.6a.)

Na rysunku D_/= (—5; 8 Y_w = (— 4; 3}.

b)    Miejsca zerowe (por. z 2-l.ób.)

Na rysunku punkty przecięcia wykresu z osią OX

to: ( — 1; O), ( ~2 ’ O J, (3.7; O). Zatem są trzy miejsca

zerowe: x, = — 1, x₂= jc₃ = 3,7.

c) Parzystość i nieparzystość (por. 2.2.3.)

Przykładowy rysunek przedstawia funkcję, która nie jest parzysta i nie jest nieparzysta, ponieważ jej wykres nie jest ani osiowo symetryczny ani środkowo symetryczny,

d) Okresowość (por. 2.2.4.)

Rysunek w 2.5.2. przedstawia funkcję, która nie jest okresowa, gdyż jej wykresu nie da się otrzymać przez powielenie ustalonego jego fragmentu. Uwaga dotycząca modułów: e). f), h).

Odpowiedzi na pytanie: gdzie? (np. gdzie funkcja rośnie, gdzie osiąga wartość najmniejszą) — szukamy na osi poziomej (OX). czyli dla jakich x. Odpowiedzi zaś na pytanie: ile? (np. ile wynosi max funkcji) — szukamy na osi pionowej (O)'), czyli chodzi o wartość funkcji, e) Znaki funkcji (por. 2.1.6c.)

Znaki funkcji, której wykres jest przedstawiony na rysunku w 2.5.2., można zilustrować następująco:

(A«2)nO)    (/(Xj)=>0)

-+    . A*>

dolna

—3 —2—10    1    2

Funkcja jest monofoniczna w niektórych przedziałach:

—    funkcja rośnie (/ /*) w trzech następujących przedziałach: dlax e (—5; —4),x G (O; 3).x € (7;8)

—    funkcja maleje (/ \.) w trzech następujących przedziałach: dla -v €= (—3; O), x €= (3; 4), .v e (5:7).

g) Rożnowartośclowość (por. 2.2.1-)

Rysunek w 2.5.2. przedstawia wykres funkcji, która nie jest różnowartościowa (istnieje pozioma prosta mająca z wykresem więcej niż jeden punkt wspólny).

h) Ekstremum, wartość nąj większa i najmniejsza funkcji (por. 2.1.6e.)

Przykładowy rysunek w 2.5.2. przedstawia wykres funkcji, która na przykład dla -^{v =} ^ osiąga minimum lokalne równo /(O) =-2. Nic jest to jednak wartość najmniejsza, gdyż istnieje od mej wartość mniejsza niż —2, na przykład dla v = 7 funkcja osiąga wartość jeszcze mniejszą. bo równą ^(7) =-4.

Na rysunku mamy; dla a = 3. f ( 3) » ' »to jest największa wartość fuitkcji (większej nic mak a dh a- 7, 7 (7) -k i to jest najmniejsza wartość

funkcji (mniejszej nie nut).

Zatem wartości największej na wykresie

i punkt ( V. --»)